Если разность четвертого и второго членов геометрической прогрессии равна 18, а разность пятого и третьего членов равна 36, то определите первого члена этой прогрессии.
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что , то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что (при этом подразумевая, что )
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: )
Возможно, это не очень явно, поэтому вспомним, что по предположению , и доделаем:
А это прямо яркий пример противоречия: предположив, что , мы получили .
Из этого следует, что , но и из предположенного же уже следует, что .
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что (при этом )
И тогда уже точно исходя из пунктов 1) и 2), получаем
В решении задачи используем очень сложную формулу (шучу):
где U - скорость тела, S - расстояние, которое тело, T - время, за которое тело преодолело расстояние.
2 тела (автомобиля) выехали из одной точки в противоположные стороны.
Первый автомобиль преодолел за 5 часов S1=U1*t, или S1 =5x (потому что х - скорость первого автомобиля, а требуемое время - 5 часов (S1 - расстояние, которое преодолел первый автомобиль, а U1 - скорость первого автомобиля))
Второй автомобиль преодолел за 5 часов S2=U2*t, или S2 =5(x+15) (потому что скорость первого автомобиля на 15 больше первого, у первого - х, значит у второго - 15+х, а требуемое время - 5 часов (S2 - расстояние, которое преодолел второй автомобиль, а U2 - скорость второго автомобиля))
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что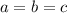 , то есть
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что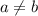 (при этом подразумевая, что
(при этом подразумевая, что 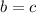 )
)
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: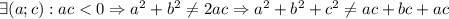 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению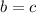 , и доделаем:
, и доделаем:
А это прямо яркий пример противоречия: предположив, что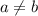 , мы получили
, мы получили 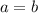 .
.
Из этого следует, что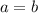 , но и из предположенного же
, но и из предположенного же 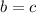 уже следует, что
уже следует, что 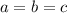 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что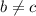 (при этом
(при этом 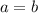 )
)
И тогда уже точно исходя из пунктов 1) и 2), получаем
S = 5(15+2x)
Объяснение:
В решении задачи используем очень сложную формулу (шучу):
2 тела (автомобиля) выехали из одной точки в противоположные стороны.
Первый автомобиль преодолел за 5 часов S1=U1*t, или S1 =5x (потому что х - скорость первого автомобиля, а требуемое время - 5 часов (S1 - расстояние, которое преодолел первый автомобиль, а U1 - скорость первого автомобиля))
Второй автомобиль преодолел за 5 часов S2=U2*t, или S2 =5(x+15) (потому что скорость первого автомобиля на 15 больше первого, у первого - х, значит у второго - 15+х, а требуемое время - 5 часов (S2 - расстояние, которое преодолел второй автомобиль, а U2 - скорость второго автомобиля))
Складываем получившиеся выражения:
S = S1 + S2 = 5x + 5(x+15) = 5(x+15+x) = 5(15+2x)