(см. объяснение)
Объяснение:
Выполним запись:
Тогда верно, что:
Значит неравенство можно переписать:
Верность этого неравенства очевидна для любого , а значит и исходное неравенство верно.
Доказано!
(см. объяснение)
Объяснение:
Выполним запись:
Тогда верно, что:
Значит неравенство можно переписать:
Верность этого неравенства очевидна для любого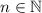 , а значит и исходное неравенство верно.
, а значит и исходное неравенство верно.
Доказано!