Прямоугольник со сторонами 8 см и 4 см вращаешься вокруг своей меньшей стороны найди площадь боковой поверхности образующегося цилиндра. Вычисли площадь боковой поверхности цилиндра, полученного при вращение прямоугольника вокруг его большой стороны. Сравни результаты.

Показать ответ

Ответ:

mariyaarif

23.03.2022 14:04

0,375

Пошаговое объяснение:

У нас есть 5 позиций: _ _ _ _ _. Посчитаем количество всех возможных на первую позицию можно поставить любую из 9 цифр, на вторую — любую из оставшихся 8, на третью — любую из оставшихся 7 и т. д., то есть всех возможных

Посчитаем количество подходящих На последней позиции должна быть нечётная цифра, на первой — 4, 5, 6 ... 9 (любая из них), а на остальных могут быть любые из оставшихся. Начнём с последней позиции: если мы поставим 1 или то на первую позицию можем поставить Тогда в этом случае подходящих Если на последнюю позицию поставим 5, 7 или то на первую позицию мы можем поставить только 5 цифр. И тогда подходящих Итого в обоих случаях 2·6·7·6·5 + 3·5·7·6·5 = 7·6·5·(2·6 + 3·5) = 7·6·5·27.

Рассчитаем вероятность: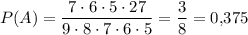 $P(A)=\dfrac{7\cdot6\cdot5\cdot27}{9\cdot8\cdot7\cdot6\cdot5}=\dfrac{3}{8}=0{,}375$

0,0(0 оценок)

Ответ:

1234567890987078

29.02.2020 20:26

Пошаговое объяснение: Дано: ∠РАО=30°, h=PO=2 м. Найти а) а)Площадь основания S

б) площадь боковой поверхности S'

в) площадь полной поверхности S''

г) объем конуса V

Решение: 1) из ΔРАО-прямоугольного имеем РО/РА=Sin30° ⇒ PA=PO/Sin30° ⇒ l=PA=2/(1/2)=4 (дм) 2) R=OA, по т. Пифагора ОА²=PA²- PO²= 4² - 2²=16- 4 = 12, ⇒ OA=√12= 2√3, ⇒ R=2√3 (дм) 3) а)Площадь основания S=πR² = π·12=12π (дм²)

б) площадь боковой поверхности S' = πrl = π·2√3·4= 8π√3 (дм²)

в) площадь полной поверхности S'' =S + S'=πR²+ πRl= 12π+8π√3=4π(3+2√3) дм²

г) объем конуса V = 1/3 ·S·h= 1/3 · 12π · 2= 8π (дм³)