Найди сумму всех двухзначных чисел, которые делятся на 10 и не делятся на 3
На 10 делятся все числа, оканчивающиеся 0.
Выпишем все такие двузначные числа:
10
20
30
40
50
60
70
80
90
Целое число делится на 3, если сумма его цифр делится на 3, в другом случае - нацело на 3 оно не делится.
10 (1 + 0 = 1) не делится
20 (2 + 0 = 2) не делится
30 (3 + 0 = 3) делится
40 (4 + 0 = 4) не делится
50 (5 + 0 = 5) не делится
60 (6 + 0 = 6) делится
70 (7 + 0 = 7) не делится
80 (8 + 0 = 8) не делится
90 (9 + 0 = 9) делится
Исключим те, которые делятся на 3 и найдем сумму оставшихся:
10 + 20 + 40 + 50 + 70 + 80 = 270
ответ: 270
Признаки делимости числа на :
Число делится на , если его конечная цифра .
Число делится на , если сумма его цифр делится на 3.
------------------------------------------------------------------------------------------------------
Так как нужны все двузначные числа, которые делятся на , то подойдут следующие числа : .
Но у нас есть ещё требование! Число не должно делиться на .
В таком случае, нам нужно отобрать все числа, делящиеся на , но не делящиеся на , по признакам делимости числа на 3.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
не делится на , т.к. сумма его цифр не делится на 3.
делится на , т.к. сумма его цифр делится на 3.
Итак, двузначные числа, делящиеся на , но не делящиеся на :
Значит, их сумма составляет :
Найди сумму всех двухзначных чисел, которые делятся на 10 и не делятся на 3
На 10 делятся все числа, оканчивающиеся 0.
Выпишем все такие двузначные числа:
10
20
30
40
50
60
70
80
90
Целое число делится на 3, если сумма его цифр делится на 3, в другом случае - нацело на 3 оно не делится.
10 (1 + 0 = 1) не делится
20 (2 + 0 = 2) не делится
30 (3 + 0 = 3) делится
40 (4 + 0 = 4) не делится
50 (5 + 0 = 5) не делится
60 (6 + 0 = 6) делится
70 (7 + 0 = 7) не делится
80 (8 + 0 = 8) не делится
90 (9 + 0 = 9) делится
Исключим те, которые делятся на 3 и найдем сумму оставшихся:
10 + 20 + 40 + 50 + 70 + 80 = 270
ответ: 270
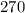
Пошаговое объяснение:Признаки делимости числа на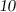 :
:
Число делится на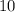 , если его конечная цифра
, если его конечная цифра 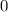 .
.
Признаки делимости числа на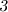 :
:
Число делится на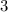 , если сумма его цифр делится на 3.
, если сумма его цифр делится на 3.
------------------------------------------------------------------------------------------------------
Так как нужны все двузначные числа, которые делятся на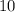 , то подойдут следующие числа :
, то подойдут следующие числа : 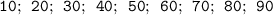 .
.
Но у нас есть ещё требование! Число не должно делиться на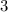 .
.
В таком случае, нам нужно отобрать все числа, делящиеся на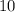 , но не делящиеся на
, но не делящиеся на 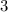 , по признакам делимости числа на 3.
, по признакам делимости числа на 3.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Итак, двузначные числа, делящиеся на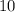 , но не делящиеся на
, но не делящиеся на 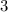 :
:
Значит, их сумма составляет :