Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=3 см ⇒
Диаметр АС=АМ+МС= см⇒
см
Как видно на рисунке, правильный шестиугольник можно поделить на 6 правильных треугольников (равносторонних)
Учитывая, что все стороны равны, то можно сказать, что S правильного шестиугольника больше в 6 раз S правильного треугольника.
Доказать это можно через формулы площадей:
Площадь правильного треугольника:
Площадь правильного шестиугольника:
или другими словами (первая формула является результатом сокращения второй)
Поделив формулу площади шестиугольника на формулу площади треугольника, получаем
(т.к. все остальное сокращается)
Таким образом, если стороны правильного шестиугольника и стороны правильного треугольника равны, то площадь шестиугольника больше в 6 раз
Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=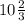 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=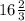 см⇒
см⇒
Как видно на рисунке, правильный шестиугольник можно поделить на 6 правильных треугольников (равносторонних)
Учитывая, что все стороны равны, то можно сказать, что S правильного шестиугольника больше в 6 раз S правильного треугольника.
Доказать это можно через формулы площадей:
Площадь правильного треугольника:
Площадь правильного шестиугольника:
Поделив формулу площади шестиугольника на формулу площади треугольника, получаем
Таким образом, если стороны правильного шестиугольника и стороны правильного треугольника равны, то площадь шестиугольника больше в 6 раз