Даны вершины треугольника: А(1;-3;4), В(2;-2;5), C(3;1;3).
Находим векторы и их модули.
АВ = (1; 1; 1), |AB| = √(1² + 1² + 1²) = √3.
BC = (1; 3; -2), |AB| = √(1² + 3² + (-2)²) = √14.
АC = (2; 4; -1), |AB| = √(2² + 4² + (-1)²) = √21.
Косинусы углов находим по формуле:
cos A = (b² + c² - a²)/(2bc).
Вот результаты расчёта:
Треугольник АВС
a(ВС) b(АС) c(АВ) p 2p S
3,741657387 4,582575695 1,732050808 5,028141945 10,05628389 3,082207001
14 21 3
1,286484558 0,44556625 3,296091137 1,889365914 9,5 3,082207001
cos A = 0,629941 cos B = -0,308607 cos С = 0,933139
Аrad = 0,889319 Brad = 1,884524 Сrad = 0,367749
Аgr = 50,954246 Bgr = 107,975284 Сgr = 21,07047.
Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора:
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Даны вершины треугольника: А(1;-3;4), В(2;-2;5), C(3;1;3).
Находим векторы и их модули.
АВ = (1; 1; 1), |AB| = √(1² + 1² + 1²) = √3.
BC = (1; 3; -2), |AB| = √(1² + 3² + (-2)²) = √14.
АC = (2; 4; -1), |AB| = √(2² + 4² + (-1)²) = √21.
Косинусы углов находим по формуле:
cos A = (b² + c² - a²)/(2bc).
Вот результаты расчёта:
Треугольник АВС
a(ВС) b(АС) c(АВ) p 2p S
3,741657387 4,582575695 1,732050808 5,028141945 10,05628389 3,082207001
14 21 3
1,286484558 0,44556625 3,296091137 1,889365914 9,5 3,082207001
cos A = 0,629941 cos B = -0,308607 cos С = 0,933139
Аrad = 0,889319 Brad = 1,884524 Сrad = 0,367749
Аgr = 50,954246 Bgr = 107,975284 Сgr = 21,07047.
Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: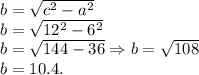
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).