На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
1)Чтобы найти площадь боковой поверхности призмы нужно найти площадь одного прямоугольника (6*9=54) и умножить на количество прямоугольников (54*4=216) Площадь боковой поверхности равен 216 см^2
Площадь всей поверхности равна сумме площади оснований (в основании лежит квадрат и его площадь равна =36 и умножаем на 2, т.к их два 36*2=72) и боковой поверхности (216+72=288) Площадь всей поверхности призмы равна 288 см^2.
2) С теоремы пифагора находим половину стороны квадрата, лежащего в основании пирамиды. (
Находим площадь одного треугольника (S=1/2*a*h, где а-сторона квадрата, h- высота треугольника(в данной задаче, апофема)
S=1/2*16*10=80 и умножаем на кол-во треугольников 80*4=320см^2
3) Чертим диагональ в основании, и диагональ основания, диагональ призмы и ребро призмы образуют прямоугольный треугольник, который будет является и равнобедренным, т.к два угла будут равны (45+x+90=180, x=45)
Находим диагональ прямоугольника по теореме пифагора (,это и будет являться высотой призмы.
Находим площади боковых прямоугольников и складываем (6*10+6*10+8*10+8*10=280см^2) Площадь боковой поверхгости призмы равно 280 см^2.
2. ∠AOC = 120°; ∠BOC = 180°; ∠ACB = 30°
3. CD = 30 см; AB = 60 см
Объяснение:
2. Упростим соотношение дуг: 3:9:6 <=> 1:3:2 <=> AB, BC, AC
Найдём их градусную меру:
AB + BC + AC = x + 3x + 2x = 360°
6x = 360°
x = 60°
AB - 60°
BC - 180°
AC - 120°
Отразим это на рисунке.
Легко видеть, что
∠AOC = 120°; ∠BOC = 180°
На рисунке видно, что отрезок AO разделяет треугольник ABC на треугольник AOB и равнобедренный AOC. Поскольку сумма углов треугольника 180°, а угла у основания равнобедренного треугольика равны, то ∠ACB = (180° - 120°)/2 = 60°/2 = 30°
3. Рисунок и решение на фото.
1)216 cm^2 и 288 cm^2 2)320 cm^2 3)280 cm^2
Объяснение:
1)Чтобы найти площадь боковой поверхности призмы нужно найти площадь одного прямоугольника (6*9=54) и умножить на количество прямоугольников (54*4=216) Площадь боковой поверхности равен 216 см^2
Площадь всей поверхности равна сумме площади оснований (в основании лежит квадрат и его площадь равна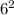 =36 и умножаем на 2, т.к их два 36*2=72) и боковой поверхности (216+72=288) Площадь всей поверхности призмы равна 288 см^2.
=36 и умножаем на 2, т.к их два 36*2=72) и боковой поверхности (216+72=288) Площадь всей поверхности призмы равна 288 см^2.
2) С теоремы пифагора находим половину стороны квадрата, лежащего в основании пирамиды. (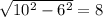
Находим площадь одного треугольника (S=1/2*a*h, где а-сторона квадрата, h- высота треугольника(в данной задаче, апофема)
S=1/2*16*10=80 и умножаем на кол-во треугольников 80*4=320см^2
3) Чертим диагональ в основании, и диагональ основания, диагональ призмы и ребро призмы образуют прямоугольный треугольник, который будет является и равнобедренным, т.к два угла будут равны (45+x+90=180, x=45)
Находим диагональ прямоугольника по теореме пифагора (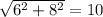 ,это и будет являться высотой призмы.
,это и будет являться высотой призмы.
Находим площади боковых прямоугольников и складываем (6*10+6*10+8*10+8*10=280см^2) Площадь боковой поверхгости призмы равно 280 см^2.