Площадь параллеограмма равна 72 см2, высоты 4 см и 6 см.найдите периметр этого паралеограмма.2) найдите площадь прямоугольного треугольника, если его катеты равны: 1) 12 см и 18 см, 2) 45 дм и 14 см.3) найдите, стороны ромба, зная что его диогонали относятся как 1: 2 , а площадь ромба равна 32 см2.(4) площадь прямоугольной трапейций равна 30 см2, а периметр 28 см. найдите большую боковую сторону, если меньшая боковая сторона равна 3 см.(5) в четыпехугольнике авсd bd=12 см.величина в удалена от стороны ас на 4 см.найдите площадь треугольника авс.
Объяснение:
Вариант 1
Часть А
1
S=1/2×a×h
a=5+3=8
h=6
S=1/2×8×6=24
ответ : 1) 24
Часть В
2
а=12 см
b=5 см
d=корень (а^2+b^2)=корень (12^2+5^2)=
=корень 169=13 см
Часть С
3
Боковая сторона b=15 cм
Высота h=9 cм
Основание а=?
а/2=корень (b^2-h^2)=корень (15^2-9^2)=
=корень144=12 см
а=12×2=24 см
4
S=(a+b)/2×h
a=17 cм
b=5 cм
c=10 cм
Х=(а-b) /2=(17-5)/2=6 cм
h=корень (с^2-Х^2)=корень (10^2-6^2)=
=корень 64=8 см
S=(17+5)/2×8=88 cм^2
5
AB=CD=x
BC=AD=3x
ВD^2=AB^2+AD^2
20^2=x^2+(3x)^2
400=x^2+9x^2
400=10x^2
X^2=40
X=корень40
АВ=СD=корень 40
ВС=АD=3корень40
S=1/2×AD×AB=1/2×3 корень40×корень40=
=1/2×3×40=60
S=1/2×BD×AH
2S=BD×AH
AH=2S/BD
AH=2×60/20=6
ответ : 6
1.
∆АВС≈∆AMK по 3-ём углам (∠А-общий, ∠AMK=∠ABC как соответственные при секущей AB и MK║BC, ∠AKM=∠ACB как соответственные при секущей AC и MK║BC) ⇒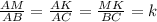
AM/AB=4/6=MK/BC=8/x x=6·8:4=12 см - BC
AM/AB=4/6=AK/AC=9/y y=6·9:4=13,5 см - AC
ответ: 12 см - BC и 13,5 см - AC
2.
По свойству медиан в треугольнике:
BO=8=2x ⇒ OK=x=4 см
AD=3х=24 ⇒ OD=x=8 см, а AO=2x=16 см
ответ: ОК=4; АО=16; ОD=8
3.
ВD - биссектриса ∆АВС ⇒
Пусть DA=x, тогда DC = 11-x
Составим пропорцию: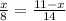
14x=88-8x
14x+8x=88
22x=88
x=4 см - сторона AD
11-4=7 cм- сторона DC
ответ: 4 см - сторона AD и 7 cм- сторона DC