Окружность, проходящая через вершины A, B и C трапеции ABCD с основаниями AD и BC, вторично пересекает прямую AD в точке M.
а) Докажите, что AC = BM.
б) Найдите AC, если AD =16, CD =8
p
3 и ∠AMB=60◦

Показать ответ

Ответ:

Леша119

21.06.2020 21:25

1-б 2-д 3-а 4-в

Объяснение:

Трапеция равносторонняя, диагональ делит угол на пополам и эта же половинка угла будет в треугольнике ABC ∠C => ABC равнобедренный. То есть бочные стороны и меньшая основа равны => x+x+x+12=52 находим что x=10. Отсюда находим большую основу, средняя линия это меньшая основа+большая основа/2 (10+22)/2=16. Рисуем 2 высоты, видим что большая основа поделилась на 3 отрезка, центральный из них равен меньшей основе, то есть 10. Понимаем что 2 других отрезка равны 12 см, а значит каждый из них по 6. За теоремой пифагора ищем высоту (любую), она будет являться катетом, обозначим как x.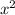 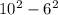$x^{2}$ = $10^{2} - 6^{2}$ , x=8

0,0(0 оценок)

Ответ:

Shrhfhd

21.06.2020 21:25

У меня с украинским не очень, поэтому...

Одна из основ трапеции на 12 см больше другой а периметр трапеции равен 52 см (см. рис). Диагональ трапеции делит острый угол пополам. Установите соответствие между отрезком и его длиной

Отрезок:

1. Меньшее основание трапеции

2. Большая основа трапеции

3. Высота трапеции

4. Средняя линия трапеции

Длина:

А) 8 см

Б) 10 см

В) 16 см

Г) 20 см

Д) 22 см

------------

Биссектриса острого угла трапеции отсекает от трапеции равнобедренный треугольник. Если эта биссектриса является и диагональю трапеции, то малое основание трапеции боковой стороне

В условии задания не сказано, что трапеция равнобедренная, но все цифирки даны именно из этого предположения!

Считаем трапецию равнобедренной. Тогда из условия, что одно основание длиннее другого на 12 см получаем

x + x + x + x + 12 = 52

x = 10 см

1. Меньшее основание трапеции

ВС = x = 10 см

2. Большее основание трапеции

АД = х + 12 = 10 + 12 = 22 см

3. Высота находится сложнее

Проекции боковых рёбер на основание равны

АГ = ЕД

ГЕ = 10 см