ответ: ∞
Объяснение:
a)
В этом задании требуется найти определенный интеграл на отрезке x ∈ (1,3). Находим первообразную:
Подставляем в нее границы интегрирования, чтобы найти определенный интеграл:
б)
Тоже самое что и в задании а). Находим первообразную функции:
Подставляем в первообразную границы интегрирования. Они определяются через пресечение параболой оси OY:
Мы получили, что нет таких точек, которые бы удовлетворяли уравнению, а значит, нет пересечения с OY и площадь ⇒∞.
в)
Находим первообразные для каждой из написанных функций:
Теперь находим пересечение двух графиков функций. Это и будут границы интегрирования:
Находим площади под каждой из двух функций при определенного интеграла:
Теперь, чтобы найти общую площадь фигуры вычитаем из большей площади меньшую:
ответ: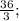 ∞
∞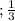
Объяснение:
a)
В этом задании требуется найти определенный интеграл на отрезке x ∈ (1,3). Находим первообразную:
Подставляем в нее границы интегрирования, чтобы найти определенный интеграл:
б)
Тоже самое что и в задании а). Находим первообразную функции:
Подставляем в первообразную границы интегрирования. Они определяются через пресечение параболой оси OY:
Мы получили, что нет таких точек, которые бы удовлетворяли уравнению, а значит, нет пересечения с OY и площадь ⇒∞.
в)
Находим первообразные для каждой из написанных функций:
Теперь находим пересечение двух графиков функций. Это и будут границы интегрирования:
Находим площади под каждой из двух функций при определенного интеграла:
Теперь, чтобы найти общую площадь фигуры вычитаем из большей площади меньшую: