уравнения без ветвлений:
а) x – а = 0
ответ:
б) 5x = а
ответ:
в) x : 2 = а
ответ:
г) x = а
ответ:
д) x3 = а
ответ уравнения с ветвлениями:
а) аx = 10
ответ:
б) 0x = а
ответ:
в) x =
а
ответ:
г) х = а
ответ:
д) (а2 – 4)x = а2 + а – 6
Решение ОТДОЮ ВСЕ ЧТО ЕСТЬ

Показать ответ

Ответ:

ArtRavi

07.09.2022 13:56

Это произведение оканчивается 18-ю нулями.

Объяснение:

Как лучше записать вычисления- смотри в конце, а пока я объясню их смысл на словах.

Дело в том, что ноль в конце произведения простых множителей может дать только пара из множителей 2 * 5 (= 10). И сколько этих пар будет- столько и нулей в конце произведения.

Поэтому, количество нулей в конце произведения можно найти и не вычисляя полностью само произведение, а следуя по такому алгоритму:

1) разложить каждый множитель произведения на простые множители

2) если нужно- упростить полученное выражение (каждый простой множитель должен быть записан один раз, в виде степени с соответствующим показателем

3) у простых множителей 2 и 5 смотрим их показатели степеней - меньшее из этих двух чисел и будет равно количеству нулей, на которое будет оканчиваться всё произведение

4) если нет хотя бы одного из этих множителей- двойки или пятёрки или обоих вместе- значит не будет и нулей в конце произведения (можно считать, что показатель степени отсутствующего множителя равен нулю, а значит (смотри пункт 3) не будет и нулей в конце произведения)

Нахождение количества нулей в конце произведения лучше всего записать виде вот такого преобразования (может быть это даже понятнее, чем выше описанный алгоритм):

$\displaystyle 15*2^{21}*5^{17}=3^1*5^1*2^{21}*5^{17}=3^1*2^{21}*5^{18}=3^1*2^{3}*2^{18}*5^{18}=\\=3^1*2^{3}*(2*5)^{18}=3*8*10^{18}=24*10^{18}$

На этом преобразования можно закончить, само произведение думаю писать не обязательно в виде единого числа, т.к. количество нулей в его конце ясно видно в показателе степени десятки.

Ну если уж хочется, то можно и написать его в конце преобразований:

= 24 000 000 000 000 000 000

0,0(0 оценок)

Ответ:

ефим30

20.06.2021 12:27

$f(x)=\left\{\begin{array}{l}2^{x}\ ,\ \ x\leq 0\ ,\\-x^2\ ,\ \ 0$

Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .

$a)\ \ \lim\limits _{x \to 0-0}f(x)=\lim\limits _{x \to 0-0}2^{x}=1\ \ ,\ \ \ \lim\limits _{x \to 0+0}f(x)=\lim\limits _{x \to 0+0}(-x^2)=0\\\\\lim\limits _{x \to 0-0}f(x)\ne \lim\limits _{x \to 0+0}f(x)\ \ \Rightarrow$

При х=0 функция имеет разрыв 1 рода .

$b)\ \ \lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2-0}(-x^2)=-4\ ,\ \ \lim\limits _{x \to 2+0}f(x)=\lim\limits _{x \to 2+0}(x-6)=-4\\\\f(2)=(-x^2)\Big|_{x=2}-4\\\\\lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2+0}f(x)=f(2)=-4\ \ \ \Rightarrow$

При х=2 функция непрерывна.

$c)\ \ \lim\limits _{x \to 5-0}f(x)=\lim\limits _{x \to 5-0}(x-6)=-1\\\\\lim\limits _{x \to 5+0}f(x)=\lim\limits _{x \to 5+0}3^{\frac{4x}{x-5}}=3^{+\infty }=+\infty \ \ \ \Rightarrow$

При х=5 функция имеет разрыв 2 рода .

График функции нарисован сплошной линией.

На 1 рисунке нет чертежа функции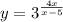 $y=3^{\frac{4x}{x-5}}$ при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .