Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Значит, 1/x - производительность первого насоса до ремонта, а 1/y - производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1
1,2(1/x) - производительность первого насоса до ремонта, а 1,6(1/y) - производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
Рассмотрим функцию . Её график представляет собой некоторую бесконечную ломаную, состоящую из частей прямых с разным углом наклона.
Даже если модули и раскроются так, чтобы перед иксами везде был плюс (получится 8x), то угол наклона всё равно будет зависеть от того, как раскроется модуль , то есть при x ≥ -1 8x-10x = -2x — функция убывает; при x < -1 8x+10x = 18x — функция возрастает. Так как больше 8x мы получить не можем, x = -1 — точка максимума этой функции. Значит, это уравнение (f(x) = 0) имеет хотя бы одно решение, если
Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Значит, 1/x - производительность первого насоса до ремонта, а 1/y - производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1
1,2(1/x) - производительность первого насоса до ремонта, а 1,6(1/y) - производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
ответ: 10 ч.
Поставь лучший ответ
Рассмотрим функцию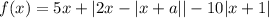
. Её график представляет собой некоторую бесконечную ломаную, состоящую из частей прямых с разным углом наклона.
Даже если модул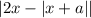и
и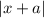 
раскроются так, чтобы перед иксами везде был плюс (получится 8x), то угол наклона всё равно будет зависеть от того, как раскроется модуль 
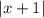, то есть при x ≥ -1 8x-10x = -2x — функция убывает; при x < -1 8x+10x = 18x — функция возрастает. Так как больше 8x мы получить не можем, x = -1 — точка максимума этой функции. Значит, это уравнение (f(x) = 0) имеет хотя бы одно решение, если
ответ:![(-\infty;-2]\cup[4;+\infty)](/tpl/images/0574/6423/c140e.png)