Всех двухэлементных подмножеств пятиэлементного множества М будет штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .
Всех двухэлементных подмножеств пятиэлементного множества М будет штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .
Почитай может что-то найдёшь.Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
a - ε < xn < a + ε которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Множество M={ 1 ,2 ,3 ,4 ,5 }
Всех двухэлементных подмножеств пятиэлементного множества М будет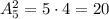
штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .
Всех двухэлементных подмножеств пятиэлементного множества М будет
штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .
Почитай может что-то найдёшь.Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
|xn - a| < ε. (6.1)
Записывают это следующим образом: или xn→ a.
Неравенство (6.1) равносильно двойному неравенству
a - ε < xn < a + ε которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Пояснення:надеюсь что-то понятно