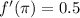Увидим константы:
Теперь пользуемся следующими правилами:
1) Константу можно вынести за знак производной
2) Производная константы равна нулю
3) Правило дифференцирования степенной функции
ответ.
Увидим константы: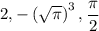
Теперь пользуемся следующими правилами:
1) Константу можно вынести за знак производной
2) Производная константы равна нулю
3) Правило дифференцирования степенной функции
ответ.