Объяснение:
Если
:
То
Перемножим неравенства.
Тогда равносильным будет переход к:
И учитывая что , тогда
Объяснение:
Если
:
То
Перемножим неравенства.
Тогда равносильным будет переход к:
И учитывая что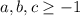 , тогда
, тогда