Эти выражения имеют смысл, пока подкоренное выражение не ушло в минус (ведь квадратный корень из отрицательного числа не извлекается, по крайней мере в действительных числах). Значит, нужно чтобы подкоренное выражение было больше или равно нулю.
x + 6 ≥ 0
далее просто решаем это неравенство- переносим числа в левую часть, меняя при этом их знак:
Просто предложено решить алгебраически систему двух уравнений.
1) х + у = 3 |*2 2 х + 2 у = 6
3 х - 2 у = - 1 3 х - 2 у = - 1 Сложим почленно: 5 х = 5,⇒ х = 1
Теперь х = 1 подставим в любое уравнение, например, в первое:
х + у = 3
1 + у = 3
у = 2
ответ: (1; 2)
2) 7 х + 4 у = 23 |*5 35x + 20y = 115
8 х + 10 у = 19| * (-2) - 16 х - 20 у = - 38 сложим почленно, получим:
19 у = 77, ⇒ у = 77/19
Теперь у = 77/19 подставим в любое уравнение, например, в первое:
7 х + 4 у = 23
7 х + 4*77/19 = 23
7 х = 23 - 308/19=129/19
х = 129/133
ответ (129/133; 77/19)
А) x ≥ -6
Б) x ≥ 4,2
Объяснение:
А)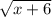
Б)
Эти выражения имеют смысл, пока подкоренное выражение не ушло в минус (ведь квадратный корень из отрицательного числа не извлекается, по крайней мере в действительных числах). Значит, нужно чтобы подкоренное выражение было больше или равно нулю.
x + 6 ≥ 0
далее просто решаем это неравенство- переносим числа в левую часть, меняя при этом их знак:
x ≥ -6 (вот и ответ на пункт А)
То есть, выражение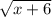
имеет смысл при x ≥ -6
x - 4,2 ≥ 0
x ≥ 4,2 (ответ на пункт Б)
То есть, выражение
имеет смысл при x ≥ 4,2