В решении.
Объяснение:
835.
Решить уравнение:
9/(x - 11) + 11/(x - 9) = 2
Умножить все части уравнения на (х - 11)(х - 9), чтобы избавиться от дробного выражения:
9 * (x - 9) + 11 * (x - 11) = 2*(х - 11)(х - 9)
Раскрыть скобки:
9х - 81 + 11х - 121 = 2х² - 18х - 22х + 198
20х - 202 = 2х² - 40х + 198
-2х² + 40х + 20х - 202 - 198 = 0
-2х² + 60х - 400 = 0
Разделить уравнение на -2 для упрощения:
х² - 30х + 200 = 0, квадратное уравнение, ищем корни:
ОДЗ: х ≠ 11; х ≠ 9;
D=b²-4ac = 900 - 800 = 100 √D=10
х₁=(-b-√D)/2a
х₁=(30-10)/2
х₁=20/2
х₁=10;
х₂=(-b+√D)/2a
х₂=(30+10)/2
х₂=40/2
х₂=20;
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
15 декабря
Можно увидеть что это задача в которой присутствует арифметическая прогрессия, в которой:
d = 4
a₁ = 10
Sₙ (сумма какого то количества первых членов) = 640
Решаем при формулы суммы n первых членов арифметической прогрессии:
Sₙ = (a1 это а₁)
Подставляем известные нам данные и решаем как уравнение:
640 =
640 = (10 + 2 * (n - 1)) * n
640 = 10n + 2n² - 2n
2n² + 8n - 640 = 0
Поделим обе части уравнения на 2 что бы упростить:
n² + 4n - 320 = 0
Найдем дискриминант:
D = 16 - 4 * 1 * (-320) = 1296
x₁ = (нам не подходит ибо количество дней не может быть отрицательным)
x₂ = (дней)
31 - 16 = 15 (декабря)
В решении.
Объяснение:
835.
Решить уравнение:
9/(x - 11) + 11/(x - 9) = 2
Умножить все части уравнения на (х - 11)(х - 9), чтобы избавиться от дробного выражения:
9 * (x - 9) + 11 * (x - 11) = 2*(х - 11)(х - 9)
Раскрыть скобки:
9х - 81 + 11х - 121 = 2х² - 18х - 22х + 198
20х - 202 = 2х² - 40х + 198
-2х² + 40х + 20х - 202 - 198 = 0
-2х² + 60х - 400 = 0
Разделить уравнение на -2 для упрощения:
х² - 30х + 200 = 0, квадратное уравнение, ищем корни:
ОДЗ: х ≠ 11; х ≠ 9;
D=b²-4ac = 900 - 800 = 100 √D=10
х₁=(-b-√D)/2a
х₁=(30-10)/2
х₁=20/2
х₁=10;
х₂=(-b+√D)/2a
х₂=(30+10)/2
х₂=40/2
х₂=20;
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
15 декабря
Объяснение:
Можно увидеть что это задача в которой присутствует арифметическая прогрессия, в которой:
d = 4
a₁ = 10
Sₙ (сумма какого то количества первых членов) = 640
Решаем при формулы суммы n первых членов арифметической прогрессии:
Sₙ =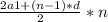
(a1 это а₁)
Подставляем известные нам данные и решаем как уравнение:
640 =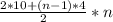
640 = (10 + 2 * (n - 1)) * n
640 = 10n + 2n² - 2n
2n² + 8n - 640 = 0
Поделим обе части уравнения на 2 что бы упростить:
n² + 4n - 320 = 0
Найдем дискриминант:
D = 16 - 4 * 1 * (-320) = 1296
x₁ =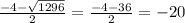
(нам не подходит ибо количество дней не может быть отрицательным)
x₂ =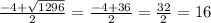
(дней)
31 - 16 = 15 (декабря)