Пусть х тонн лома, содержащего 5 % никеля, и у тонн лома, содержащего 40 %, надо взять. Получится х+у или 140 тонн. Никеля во взятом количестве содержится 0,05х+0,4у или 0,3*140 тонн. Составим и решим систему уравнений:
х+у=140
0,05х+0,4у=0,3*140
х=140-у
0,05х+0,4у=42
х=140-у
0,05(140-у)+0,4у=42
х=140-у
7-0,05у+0,4у=42
х=140-у
0,35у=35
х=140-у
у=35:0,35
х=140-у
у=100
х=140-100
у=100
х=40
у=100
ответ: чтобы получить 140 тонн стали с 30 - процентным содержанием никеля, следует взять 40 тонн лома, содержащего 5 % никеля, и 100 тонн лома, содержащего 40 % никеля.
Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через , другой - через .
Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).
Сумма корней:
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).
5 % - 0,05; 40 % - 0,4; 30 % - 0,3
Пусть х тонн лома, содержащего 5 % никеля, и у тонн лома, содержащего 40 %, надо взять. Получится х+у или 140 тонн. Никеля во взятом количестве содержится 0,05х+0,4у или 0,3*140 тонн. Составим и решим систему уравнений:
х+у=140
0,05х+0,4у=0,3*140
х=140-у
0,05х+0,4у=42
х=140-у
0,05(140-у)+0,4у=42
х=140-у
7-0,05у+0,4у=42
х=140-у
0,35у=35
х=140-у
у=35:0,35
х=140-у
у=100
х=140-100
у=100
х=40
у=100
ответ: чтобы получить 140 тонн стали с 30 - процентным содержанием никеля, следует взять 40 тонн лома, содержащего 5 % никеля, и 100 тонн лома, содержащего 40 % никеля.
Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через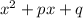 , другой - через
, другой - через 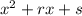 .
.
Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
Сумма корней: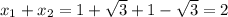
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
Сумма корней: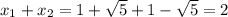
ответ: 2.