х км/ч скорость катера
(х + 1,5) км/ч скорость катера по течению
х - 1,5) км/ч скорость катера против течения
2 (х+1,5) км катер по течению реки за 2 часа
3 (х-1,5) км катер против течения реки за 3 часа
По условию известно, что за 2 часа катер проходит по течению реки в 1.25 раза меньше, чем за 3 часа против течения реки.
Получаем уравнение:
1,25 * 2 (х+1,5) = 3 (х-1,5)
2,5 (х+1,5) = 3 х - 4,5
2,5 х + 3,75 = 3 х - 4,5
3 х - 2,5 х = 8,25
0,5 х = 8,25
х = 8,25 6 0,5
х = 16,5
ответ. 16,5 км/ч скорость катера в стоячей воде
Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
решаем данное неравенство.
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
рассматриваем оба неравенства и находим область пересечения интервалов
x∈ [ +∞ [
7. значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
находим область пересечения обоих условий,
x∈ ] -∞; 7/15 [
8. область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие
x∈ ] 1; +∞ [
х км/ч скорость катера
(х + 1,5) км/ч скорость катера по течению
х - 1,5) км/ч скорость катера против течения
2 (х+1,5) км катер по течению реки за 2 часа
3 (х-1,5) км катер против течения реки за 3 часа
По условию известно, что за 2 часа катер проходит по течению реки в 1.25 раза меньше, чем за 3 часа против течения реки.
Получаем уравнение:
1,25 * 2 (х+1,5) = 3 (х-1,5)
2,5 (х+1,5) = 3 х - 4,5
2,5 х + 3,75 = 3 х - 4,5
3 х - 2,5 х = 8,25
0,5 х = 8,25
х = 8,25 6 0,5
х = 16,5
ответ. 16,5 км/ч скорость катера в стоячей воде
Объяснение:
Объяснение:
6. данная функция является сложной. корень четной степени - это значит, что значение под корнем должно быть неотрицательным. т.е.
далее, функция логарифмическая, следовательно величина под знаком логарифма должна быть больше нуля.
рассматриваем оба неравенства и находим область пересечения интервалов
7.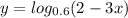 значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
значение под знаком логарифма должно быть больше нуля. 2-3х>0 2>3x x<2/3
рассмотрим условие при котором у>1
находим область пересечения обоих условий,
8.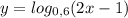 область определения функции.
область определения функции.
2х-1>0 x>1/2
вводим дополнительное условие