Решением является перебор вариантов:
Можно достать шары из урны четырьмя
1) 2 белых
2) 2 чёрных
3) 1 белый и 1 чёрный
4) сначала 1 чёрный, потом 1 белый.
Вероятности этих событий:
1)
2)
3)
4)
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:
Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:
Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.
Решением является перебор вариантов:
Можно достать шары из урны четырьмя
1) 2 белых
2) 2 чёрных
3) 1 белый и 1 чёрный
4) сначала 1 чёрный, потом 1 белый.
Вероятности этих событий:
1)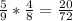
2)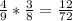
3)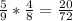
4)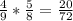
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:
Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:
Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.
Скорость течения Vт = 2 км/ч
Путь по течению:
Расстояние S₁ = 8 (км)
Скорость V₁ = Vc + Vт = х + 2 (км/ч)
Время t₁ = S₁/V₁ = 8/(x + 2) (ч.)
Путь против течения:
Расстояние S₂ = 3 (км)
Скорость V₂ = Vc - Vт = х - 2 (км/ч)
Время t₂ = S₂ /V₂ = 3/(x - 2) (ч.)
По условию t₁ + t₂ = 45 мин. = 45/60 ч. = 3/4 ч. ⇒ уравнение:
8/(х + 2) + 3/(х - 2) = 3/4 | * 4(x-2)(x +2)
x≠ -2 ; х≠ 2
32(x-2) + 12(x +2) = 3(x-2)(x +2)
32х - 64 + 12х + 24 = 3(х² - 2²)
44х - 40 = 3х² - 12
3х² - 12 - 44х + 40 = 0
3х² - 44х + 28 = 0
D = (-44)² - 4*3*28 = 1936 - 336=1600 = 40²
D>0 - два корня уравнения
х₁ = ( - (-44) - 40)/(2*3) = (44 - 40)/6 = 4/6 = 2/3 не удовл. условию задачи, т.к. собственная скорость не может быть меньше скорости течения.
х₂ = ( - (-44) + 40)/(2*3) = 84/6 = 14 (км/ч) Vc
ответ: 14 км/ч собственная скорость лодки.