110. теңдеудің графигін салыңдар:
1) 2х^2-4x-y+5=0;
2) x^2+y^2-x+5y+1/4=0
3) x^2+y^2-8/3y-20/9=0
4) x^2-8x-y+13=0.

Показать ответ

Ответ:

MashaYamg

25.02.2023 15:02

Событие А- "студент ответил хотя бы на 1 из 2 вопросов" значит, что студент ответил на один вопрос или на два.

Испытание состоит в том, что из 20-ти вопросов выбирают два.

n=C²₂₀=20!/((20-2)!·2!)=190

Событие M- "студент ответил на 1 из 2 вопросов"

Событию М благоприятствуют те случаи, когда один вопрос выбран из 16-ти выученных, а второй вопрос из четырех невыученных.

m=C¹₁₆·C¹₄=16·4=64

По формуле классической вероятности

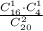p(M)=m/n= $\frac{C^1_{16}\cdot C^1_{4}}{C^2_{20}}$ -

вероятность того, что студент ответил на один вопрос из двух

Событие N- "студент ответил на 2 из 2 вопросов"

Событию N благоприятствуют те случаи, когда два вопроса выбраны из 16-ти выученных.

m=C²₁₆·C⁰₄=16!/((16-2)!·2!)=120

По формуле классической вероятности

p(N)=m/n=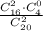 $\frac{C^2_{16}\cdot C^0_{4}}{C^2_{20}}$ -

вероятность того, что студент ответил на два вопроса из двух.

р(А)=p(M)+p(N)=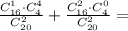 $\frac{C^1_{16}\cdot C^4_{4}}{C^2_{20}}+\frac{C^2_{16}\cdot C^0_{4}}{C^2_{20}}=$

$=\frac{64}{190}+\frac{120}{190}=\frac{184}{190}=\frac{92}{95}$

Событие В- "студент не ответил хотя бы на 1 из 2 вопросов", значит не ответил на один или не ответил на два.

Событие M- "студент ответил на 1 из 2 вопросов" означает, что на один ответил, а на другой не ответил.

p(M)=m/n=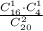 $\frac{C^1_{16}\cdot C^1_{4}}{C^2_{20}}$ -

Событие K- "студент не ответил на 2 из 2 вопросов"

Событию N благоприятствуют те случаи, когда два вопроса выбраны из 4-х невыученных.

m=C⁰₁₆·C²₄=4!/((4-2)!·2!)=6

По формуле классической вероятности

p(K)=m/n=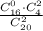 $\frac{C^0_{16}\cdot C^2_{4}}{C^2_{20}}$

p(B)=p(M)+p(K)=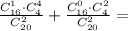 $\frac{C^1_{16}\cdot C^4_{4}}{C^2_{20}}+\frac{C^0_{16}\cdot C^2_{4}}{C^2_{20}}=$

$=\frac{64}{190}+\frac{6}{190}=\frac{70}{190}=\frac{7}{19}$

0,0(0 оценок)

Ответ:

natashashvachka

07.04.2023 00:03

Покажем, что (cos x)'=-sin x

По определению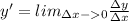 $y'=lim_{\Delta x-0} \frac {\Delta y}{\Delta x}$

Приращение функции равно

$\Delta y=cos (x+\Delta x)-cos x=-2sin(x+\frac{\Delta x}{2})sin (\frac {\Delta x}{2})$

Ищем отношение

$\frac {\Delta y}{\Delta x}=-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}$

Перейдем в этом равенстве к границе, когда $\Delta x-0$ . В следствии непрерывности функции sin x

$lim_{\Delta x-0} -sin(x+\frac{\Delta x}{2})=- -sin lim_{\Delta x-0}(x+\frac{\Delta x}{2})=-sin x$

Для второго множителя (используя один из замечательных пределов), обозначив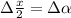 $\Delta \frac {x}{2} =\Delta \alpha$ , имеем

$lim_{\Delta x-0} \frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}= lim_{\alpha-0} \frac {sin \alpha}{\alpha}=1$

Поєтому

$lim_{\Delta x-0} \frac {\Delta y}{\Delta x}=lim_{\Delta x-0} (-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}})=-sin x *1=-sin x$

Т.е. (сos x)'=-sinx

Производная тангенса. Возьмем любую точку х є (a;b), где (a;b) - один из интервалов, на котором определена функция tg x. Ищем приращение

$\Delta y=\frac {sin (x+\Delta x)}{cos(x+\Delta x)}-\frac {sin x}{cos x}= =\frac{sin(x+\Delta x)cos x-sinx cos(x+\Delta x)}{cos(x+\Delta x)cos x}= \frac{sin \Delta x}{cos(x+\Delta x)cos x}$