1. ерейди от математической модели к словесной.
{9x+4y=905y−3=7x
коров и 4 лошадей ежедневно вместе получали 90 кг сена.
Сколько сена ежедневно скармливали каждой корове и каждой лошади, если 7 коров получали сена на 3 кг , чем 5 лошадей?
(В первое окошко введи число, а не слово.)
2. Составь математическую модель по словесной.
Соседка разводит кур и кроликов.
Сколько у соседки кур и сколько кроликов, если у них вместе 52 голов и
164 лап(-ы)?
Выбери подходящую математическую модель, обозначив
число кур за x, а число кроликов за y:
{x+y=522x+4y=164
{x+y=5212xy=164
{(x+y)⋅2=164y:x=2
{x+y=52(x+y)⋅2=164
другой ответ
{x⋅y=216x+y=52
3.Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 360 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 650 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?
4. Составь словесную модель по математической.
{5x+2y=16,72x+7y=16,6
1. Введём обозначения.
Пусть x
ткани необходимо для пошива одного мужского и
метров ткани — для пошива одного детского пальто.
2. Перейдём к словесной модели.
Из 16,7 м ткани можно сшить 5 мужских и
детских пальто.
Сколько метров ткани необходимо для пошива одного мужского и одного детского пальто,
если из
м той же ткани можно сшить 2 мужских и
детских пальто?
(Заполни пустые окошки.)
5. Создай систему для решения задачи.
Двое рабочих вместе изготовили 320 деталей.
Первый рабочий работал 5 дня(-ей), а второй — 4 дня(-ей).
Сколько деталей изготавливал каждый рабочий за один день, если второй рабочий за 2 дня изготавливал на 60 деталей меньше, чем первый рабочий за 3 дня?
Пусть x деталей в день изготавливал первый рабочий, а второй —
y деталей в день. Выбери подходящую математическую модель:
{5x+4y=3203x=2y−60
другой ответ
{x+y=320:93x=2y−60
{3x−60=2y9(x+y)=320
{5x+4y=3203x−60=2y
{3x+60=2y5x+4y=320
6. В первой ёмкости на 4 л молока больше, чем во второй.
Если из первой ёмкости перелить во вторую 13 л молока, то во второй ёмкости станет в 2 раза больше, чем останется в первой.
Сколько литров молока в каждой ёмкости?
ответ: в первой ёмкости
литра(-ов) молока, а
во второй ёмкости
литра(-ов) молока.
ответ: 180
Объяснение:
Мы знаем что данное трехзначное число в 20 раз больше его суммы цифр , это значит что оно делится на 20, а значит неизбежно кончается цифрой 0 , а предпоследняя его цифра должна быть четной.
Так же можно приметить такое свойство , что любое число дает тот же остаток от деления на 9 , что и его сумма цифр.
Пусть остаток от деления на 9 его суммы цифр равен p (S=9*n+p) , тогда наше число : N=20*S=9*n*20+20*p. (S-сумма цифр)
Таким образом 20*p при делении на 9 так же дает остаток p.
20*p=9*k+p
19*p=9*k
тк 19- простое число , то p делится на 9.
тк p=( 0,1,2,3...8) , то единственное p удовлетворяющее этому условию:
p=0 , другими словами такое трехзначное число должно делится на 9.
Последняя цифра 0 , а максимальная сумма двух цифр с одной четной цифрой : 8+9=17<18=2*9 .
А значит нужно искать такие цифры , чтобы их сумма была равна 9. ( тк сумма цифр должна делится на 9)
Но если сумма цифр 9 , то само число : 9*20=180
Проверим : 1+8+0=9 , верно.
Таким образом единственное трехзначное число , что удовлетворяет этому условие является : 180
В этой задаче удобно обозначить половину времени через t , тогда всё время будет 2t .
Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 16 км/ч , значит протяжённость первой половины пути :
Вторую половину времени шёл пешком со скоростью 8 км/ч , значит протяжённость второй половины пути равна :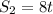
Следовательно , весь путь равен :
Средняя скорость вычисляется по формуле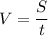
, где S - весь пройденный путь , а t - всё время , за которое этот путь пройден .
Значит :