Оценим максимальное значение, которое может принимать элемент множества . Предположим, что существуют хотя бы два элемента множества, больших . Пусть это числа . Положим , тогда , откуда . Противоречие. Значит, существует не более одного числа, большего
Теперь становится ясно, как строить множество. Пусть максимальное число равно . Тогда следующее по величине число меньше , где — текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит . Берем 47. Далее: . Берем 28. И так далее. Получим множество , состоящее из 11 элементов. Это и есть наш ответ.
Оценим максимальное значение, которое может принимать элемент множества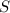 . Предположим, что существуют хотя бы два элемента множества, больших
. Предположим, что существуют хотя бы два элемента множества, больших 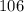 . Пусть это числа
. Пусть это числа 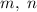 . Положим
. Положим 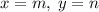 , тогда
, тогда 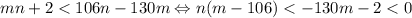 , откуда
, откуда 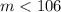 . Противоречие. Значит, существует не более одного числа, большего
. Противоречие. Значит, существует не более одного числа, большего
Теперь становится ясно, как строить множество. Пусть максимальное число равно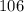 . Тогда следующее по величине число меньше
. Тогда следующее по величине число меньше 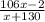 , где
, где  — текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит
— текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит 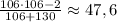 . Берем 47. Далее:
. Берем 47. Далее: 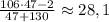 . Берем 28. И так далее. Получим множество
. Берем 28. И так далее. Получим множество 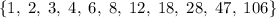 , состоящее из 11 элементов. Это и есть наш ответ.
, состоящее из 11 элементов. Это и есть наш ответ.
Чтобы решить заданное уравнение умножим уравнение на (6 3/8 - у):
7 3/4 : (6 3/8 - у) = 8 6/7;
7 3/4 = 8 6/7 * (6 3/8 - у);
6 3/8 - у ≠ 0;
у ≠ 6 3/8.
7 3/4 = 8 6/7 * 6 3/8 - 8 6/7у;
8 6/7 * 6 3/8 = (8 * 7 + 6)/7 * (6 * 8 + 3)/8 = 62/7 * 51/8 = (2 * 31 * 51)/(7 * 2 * 4) = 1581/28 = 56 13/28;
7 3/4 = 56 13/28 - 8 6/7у;
8 6/7у = 56 13/28 - 7 3/4;
56 - 7 + 13/28 - 3/4 = 49 + 13/28 - 21/28 = 49 - 8/28 = 49 - 2/7 = 48 5/7;
8 6/7у = 48 5/7;
у = 48 5/7 : 8 6/7;
у = 341/7 : 62/7;
у = 341/7 * 7/62;
у = (31 * 11)/(2 * 31);
у = 11/2;
у = 5 1/2.
ответ: у = 5 1/2.