Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
АсяБру
28.04.2021 01:39 •
Математика
Записать уравнение касательной к кривой y=4sin6x в точке с абcциссой x=p/18
Показать ответ
Ответ:
ilyashamonin
10.10.2020 20:42
Пошаговое объяснение:
Уравнение касательной:
Уравнение касательной будет иметь вид:
0,0
(0 оценок)
Популярные вопросы: Математика
Gamoo
28.11.2021 07:15
Пример 1. Округлим десятичную дробь а = 1928,3745:а) до единиц;б) до десятых;в) до сотых;г) до тысячных;г)д) до десятков;e) до сотен;ж) до тысяч.Пример 2. Округлив числа...
geliebtemutter
15.04.2023 03:25
1 4/5:(-4/5) -4/9:(-1 1/9) решите примеры...
филя24
24.07.2022 14:12
Найти другие частные производные приведенных функций....
Даша333555
11.01.2022 22:43
Задача: Определи, сколько чехлов для коньков понадобится 9 спортсменам, если у каждого конька отдельный чехол....
oslipak
11.01.2022 22:43
Дан прямоугольный равнобедренный треугольник ABC.При симметрии представленного треугольника относительно прямой, содержащей его катет AC, вершина В треугольника перешла...
эмирия
16.04.2021 05:58
Чи є рівняння лінійним рівнянням з двома змінними? (декілька варіантів відповідей)1)7х + 11у = 362)х2 + 4у = 63)12х - 17у = 04)-3х + ху = 105)0х - 5у = 0...
пончик123456798
24.04.2020 22:52
Квадрат 4х4 состоит из 16 клеток со сторо- ной 1 (см. рисунок). Қакое наибольшее число сторон клеток нужно отметить, чтобы у каждой клетки было отмечено не более двух сторон?...
sofiyabutina667
25.05.2023 20:00
Участок прямоугольной формы нужно обнести забором из металических листов. Длина участка 250 дм, а площадь 600 м2. Сколько металических листов 2 м 5 дм надо купить для этого...
dashutka20032
29.05.2022 07:44
Решение текстовых задач с уравнений. Урок 2 Целлюлоза массой 6 т содержит в себе 85% воды. Определи, сколько воды необходимо испарить, чтобы она содержала 25% целлюлозы.Выбери...
kuzmichevaliza
28.11.2022 18:55
Нужна и желательно как можно быстрее, фото идёт дополнительным условием к 3му заданию...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Пошаговое объяснение:
Уравнение касательной: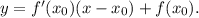
Уравнение касательной будет иметь вид: