решить: На отрезке AB взяты точки C и D так, что точка C лежит между точками A и D. Известно, что AC : CD = 4:5; CD : DB = 3:2. Найдите AC, CB и BD , если AB = 20 см.
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Пошаговое объяснение:
Точка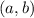
на комплексной плоскости изображает число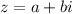 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа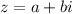
будет являться число 
.
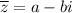В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси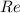
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
1) 24 : 3 = 8 (км/ч) - скорость лыжника.
ответ: 8 км/ч.
2) 80 · 4 = 320 (км) проехал мотоциклист.
ответ: 320 км.
3) 28 : 7 = 4 (ч) - была в пути лодка.
ответ: 4 ч.
4) 12 : 4 = 3 (м/с) - скорость мышки.
ответ: 3 м/с.
5) 15 : 5 = 3 (ч) - пройдет пешеход.
ответ: за 3 ч.
6) 33 : 3 = 11 (км/ч) - скорость велосипедиста.
ответ: 11 км/ч.
Формула s = v · t (s - путь, v - скорость, t - время) подходит для задачи 2.
Формула t = s / v (s - путь, v - скорость, t - время) подходит для задач 3 и 5.
Формула v = s / t (s - путь, v - скорость, t - время) подходит для задач 1, 4 и 6.