В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
ответы к/р 4 "делимость чисел"
Вариант 1
1. а) Д(33)=1;3;11;33.
б) Д(13)= 1;13.
2. К(14)= 14;28;42;56;70;…
3. а) 4302, 2880, 9164, 6020
б) 7385, 2880, 6020
в) 2880, 6020
4. а) 5532, 6786
б) 6786
5.а) да
б) да
6. а)105=3∙5∙7
б) 360=2332∙5
7. а)НОД(32;48)=16
б) НОК(16;20)=80
8. 11(ост.15)
9. а) 2194
б) 945
10.9996
Вариант 2
1. а) Д(27)=1;3;9;27.
б) Д(19)= 1;19.
2. К(15)= 15;30;45;60;75;…
3. а) 9164, 1810, 3976, 870
б) 1810, 1235, 870
в) 1810, 870
4. а) 5649, 1827
б) 1827
5.а) да
б) нет
6. а)105=2∙3∙17
б) 360=2233∙5
7. а)НОД(27;45)=9
б) НОК(15;18)=90
8. 17(ост.35)
9. а) 1040
б) 141
10. 1005
Пошаговое объяснение:
Точка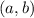
на комплексной плоскости изображает число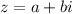 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа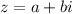
будет являться число 
.
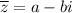В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси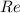
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.