Угловой коэффициент касательной равен , а значит, производная в искомой точке будет равна :
Найдём производную:
Тут не нужно раскрывать скобки, поскольку слева и справа — полный квадрат. Нам нужно только отрицательное решение, поэтому:
Получили точку с координатами –2 и 0. Их сумма –2.
ответ: –2.
На скриншоте проверка на компьютере. К этому графику есть ещё одна касательная, но она не подходит по условию (обозначил пунктиром — не надо перерисовывать).
Угловой коэффициент касательной равен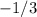 , а значит, производная в искомой точке будет равна
, а значит, производная в искомой точке будет равна 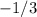 :
:
Найдём производную:
Тут не нужно раскрывать скобки, поскольку слева и справа — полный квадрат. Нам нужно только отрицательное решение, поэтому:
Получили точку с координатами –2 и 0. Их сумма –2.
ответ: –2.
На скриншоте проверка на компьютере. К этому графику есть ещё одна касательная, но она не подходит по условию (обозначил пунктиром — не надо перерисовывать).
Пошаговое объяснение:
у нас дана прямая с угловым коэффициентом у =(-1/3)х-2 .
любая ║ ей прямая будет иметь такой же угловой коэффициент -1/3
для случая касательной угловой коэффициент - значение производной в точке касания. значит, найдем производную - найдем точку касания
теперь y'(x₀)= -1/3
точка х₂ = 4 нас не интересует.
найдем точку касания с отрицательной абсциссой
у(-2) = 0, т.е. точка (-2; 0)
ответ
сумма координат точки с отрицательной абсциссой (-2; 0) равна (-2)
дополнительно можно найти уравнение касательной
проверим всё на чертеже