Насколько я понял x и y независмые переменные (т.е. y - не функция от x), тогда:
найдем
в точке экстремума дифференциал должен быть равен 0
Находим точки подозрительные на экстремум:
Получаем решения
Теперь смотрим на матрицу второго дифференциала
Она отрицательно опрделенная, т.к.
Значит x=3, y=6 - точка экстремума, а точнее точка максимума
Насколько я понял x и y независмые переменные (т.е. y - не функция от x), тогда:
найдем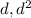
в точке экстремума дифференциал должен быть равен 0
Находим точки подозрительные на экстремум:
Получаем решения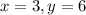
Теперь смотрим на матрицу второго дифференциала
Она отрицательно опрделенная, т.к.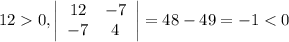
Значит x=3, y=6 - точка экстремума, а точнее точка максимума