Идентификационные номера (ID) 351 пользователей занимают в памяти 3 килобайта и 789 байт. Каждый такой ID в компьютерной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Какое минимальное количества символов может содержаться в наборе символов для создания идентификационного номера, если длина этого номера составляет 22 символа?

В ответе укажите только число - количество символов в наборе.

Мы знаем мощность алфавита (N) - 16 символов.

Нам необходимо узнать вес одного символа.

Формула нахождения мощности алфавита:

N =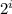 , где i - вес одного символа.

Подставим в формулу существующее значение:

16 =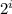

Значит, i - 4 бита, ведь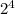 = 16.

Так, 1 символ текста кодируется 4 битами.

80 × 256 = 20480 - количество символов во всём тексте.

20480 символов = 20480 × 4 = 81920 бит

1 Килобайт = 1024 байт, а 1024 байт = 1024 × 8 = 8192 бит

81920 ÷ 8192 = 10 Килобайт

ответ: для сохранения данного текста потребуется 10 Килобайт памяти.

5 байт

Определим мощность алфавита для кодирования личного кода, по условию это 9 букв и 9 цифр,  то есть

N= 9+9 = 18 , один символ в таком случае кодируется: 5 битами (2⁵=32), т.к. 4 бит недостаточно для кодирования 18 символов ( 2⁴=16)

Всего символов в коде: k=12, значит информационный объем кода: 12*5= 60 бит. Минимальное число байт ( число кратное 8) = 8 байт

Определим объем информации для номера группы:

N=11 ⇒ i= 4 бит, минимальное число байт = 1 байт

Пропуск содержит 14 байт информации. значит объем  памяти необходимый для хранения дополнительных сведений=

14-8-1= 5 байт

Объяснение: