Это логическое выражение, где переменными выступают выражения , и . Обозначим их за , и соответственно. Например, , если , и иначе. У нас получается следующее выражение:
Раскроем импликацию и получим:
Уберём повторяющуюся . Наше финальное выражение:
Таким образом, выражение из условия будет истинно, если число не принадлежит , или не принадлежит , или принадлежит . Множество наименьшего размера будет содержать все числа, которые не удовлетворяют условию , то есть все числа, которые принадлежат и , и .
Тут четыре цикла, каждый из которых выполняет движение до конца (до тех пор, пока робот не достигнет стенки).
1) Нужно в уме представить клетки, в которые "упадут" роботы из всех начальных положений, если будут двигаться в первом направлении (вверх, до конца). Таких клеток окажется немного (см. рисунок 1).
2) Потом представляем, куда из этих клеток переместится робот при движении влево до конца. Таких клеток ещё меньше (см. рисунок 2).
3) Смотрим, куда попадём если вниз до конца. Останется одна клетка (см. рисунок 3).
4) И, двигаемся до конца вправо (см. рисунок 4).
Мы попадём в клетку E1.
Сюда будут попадать роботы из любого начального положения в этом лабиринте. Значит, единственная клетка, с которой робот может начать и в ней же закончить движение- это и есть клетка E1.
p = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
q = [3, 6, 9, 12, 15, 18, 21, 24, 27, 30]
ans = 0
for x in range(30):
if (x in p) and (x in q):
ans += x
print(ans)
Объяснение:
Это логическое выражение, где переменными выступают выражения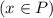 ,
, 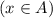 и
и 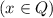 . Обозначим их за
. Обозначим их за 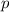 ,
,  и
и 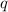 соответственно. Например,
соответственно. Например, 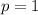 , если
, если  , и
, и 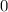 иначе. У нас получается следующее выражение:
иначе. У нас получается следующее выражение:
Раскроем импликацию и получим:
Уберём повторяющуюся . Наше финальное выражение:
. Наше финальное выражение:
Таким образом, выражение из условия будет истинно, если число не принадлежит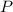 , или не принадлежит
, или не принадлежит 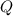 , или принадлежит
, или принадлежит 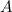 . Множество
. Множество 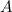 наименьшего размера будет содержать все числа, которые не удовлетворяют условию
наименьшего размера будет содержать все числа, которые не удовлетворяют условию 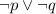 , то есть все числа, которые принадлежат и
, то есть все числа, которые принадлежат и 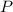 , и
, и 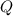 .
.
Тут четыре цикла, каждый из которых выполняет движение до конца (до тех пор, пока робот не достигнет стенки).
1) Нужно в уме представить клетки, в которые "упадут" роботы из всех начальных положений, если будут двигаться в первом направлении (вверх, до конца). Таких клеток окажется немного (см. рисунок 1).
2) Потом представляем, куда из этих клеток переместится робот при движении влево до конца. Таких клеток ещё меньше (см. рисунок 2).
3) Смотрим, куда попадём если вниз до конца. Останется одна клетка (см. рисунок 3).
4) И, двигаемся до конца вправо (см. рисунок 4).
Мы попадём в клетку E1.
Сюда будут попадать роботы из любого начального положения в этом лабиринте. Значит, единственная клетка, с которой робот может начать и в ней же закончить движение- это и есть клетка E1.