PascalABC.NET ₃.₆.₃.₂₅₇₇## var b: boolean; repeat if b then Writeln(); if b then b := False; Print('Введите 3 числа:'); var a := ArrGen(3, i -> TryRead(i) ? i : Random(1,35)); Println($'Исходные числа:', a.JoinToString(', ') + '.'); repeat Print('Что вывести на экран? (0, 1, 2, 3, 4, 5, -1):'); var x: integer; x := TryRead(x) ? x : 100; case x of 0: Println(' результат:', a.Sum); 1: Println(' результат:', a.Product); 2: Println(' результат:', Abs(a[0] - a[2])); 3: Println(' результат:', a[0] * a[2] / a[1]); 4: Println(' результат:', (a[0]**(1/2) - a[1]**(1/3)) * a[2]**4); 5: exit; -1: b := True; else Println(' неверный ввод'); end until buntil not b
Подобное выражение - развернутая форма записи числа.
Здесь, например, степени выглядит в троичной системе счисления как 1 и четыре тысячи нулей после единицы, т.е. что-то вроде . Аналогично в троичной системе счисления - это 1 и 800 нулей и так далее. Понятно, что, если единицы стоят в разных разрядах, выполнить сложение в любой системе счисления не составит труда, ведь . Собственно, говоря, очевидно и, что , но не забываем, что . Т.е. сначала выполним сложение. Еще раз замечу, что сложение выполняется в троичной системе счисления. Так, пока из 4000 нулей пропало 2, т.е. на данный момент осталось 3998 нулей. Но это еще не все. У нас есть вычитание. Вычитаем, понятно, по такому же принципу, как в десятичной системе счисления. Например, для десятичной системы счисления верно, что . Видим, что старшая единица пропадает, а нули меняются на 9, т.е. на основание системы счисления минус 1 (у нас 10-1=9). То же и в троичной системе. Например, . Соответственно, в итоге в троичной системе счисления число примет вид: , где сначала идет 2400 двоек (4000-1600), затем идет 799 нулей, затем единица, затем 799 нулей и в конце 2. ответим теперь на вопрос задачи: в троичной записи данного числа содержится 1598 нулей.
Пример работы:
1598
Объяснение:
Рассмотрим данное выражение:
Подобное выражение - развернутая форма записи числа.
Здесь, например,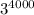
степени выглядит в троичной системе счисления как 1 и четыре тысячи нулей после единицы, т.е. что-то вроде 
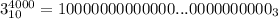. Аналогично 
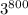в троичной системе счисления - это 1 и 800 нулей и так далее. Понятно, что, если единицы стоят в разных разрядах, выполнить сложение в любой системе счисления не составит труда, ведь 
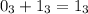. Собственно, говоря, очевидно и, что 
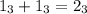, но не забываем, что 
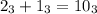. Т.е. сначала выполним сложение. Еще раз замечу, что сложение выполняется в троичной системе счисления. Так, пока из 4000 нулей пропало 2, т.е. на данный момент осталось 3998 нулей. Но это еще не все. У нас есть вычитание. Вычитаем, понятно, по такому же принципу, как в десятичной системе счисления. Например, для десятичной системы счисления верно, что 
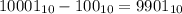. Видим, что старшая единица пропадает, а нули меняются на 9, т.е. на основание системы счисления минус 1 (у нас 10-1=9). То же и в троичной системе. Например, 
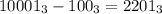. Соответственно, в итоге в троичной системе счисления число примет вид: 
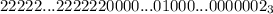, где сначала идет 2400 двоек (4000-1600), затем идет 799 нулей, затем единица, затем 799 нулей и в конце 2. ответим теперь на вопрос задачи: в троичной записи данного числа содержится 1598 нулей.
Задача решена!