Каждое основание n-угольной призмы имеет n сторон.
Ребра снования, общие с боковыми гранями, параллельны друг другу ( лежат в параллельных плоскостях) и составляют n пар двугранных углов - по одному при верхнем и нижнем основании. . Сумма этих углов при каждой грани равна сумме линейных углов при ребрах верхнего и нижнего основания.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Сумма углов, образующихся при этом у каждого ребра основания, равна сумме внутренних углов, образующихся при пересечении параллельных прямых секущей, т.е. 180°.
Следовательно, сумма двугранных углов, прилежащих к ребрам обоих оснований, равна n•180°
Для примера рассмотрим четырехугольную призму АВСDD1А1В1С1
Сумма двугранных углов КМН+ТНМ = 180°,
а сумма всех двугранных углов 4-угольной призмы равна 180•4=720°
В правильном многоугольнике все стороны и углы равны.
Внутренний угол правильного n-угольника вычисляется по формуле
ΔABC = ΔBCD по двум сторонам и углу между ними (AB=BC=CD, ∠ABC=∠BCD), поэтому AC=BD, как соответственные стороны (AC напротив ∠ABC; BD напротив ∠BCD и эти углы равны).
ΔABD = ΔDCA по трём сторонам (AB=DC, AC=DB и AD - общая), поэтому ∠BAD=∠CDA, как соответственные углы (∠BAD напротив BD; ∠CDA напротив AC и эти стороны равны).
Сумма углов в выпуклом четырёхугольнике равна 360°.
Каждое основание n-угольной призмы имеет n сторон.
Ребра снования, общие с боковыми гранями, параллельны друг другу ( лежат в параллельных плоскостях) и составляют n пар двугранных углов - по одному при верхнем и нижнем основании. . Сумма этих углов при каждой грани равна сумме линейных углов при ребрах верхнего и нижнего основания.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Сумма углов, образующихся при этом у каждого ребра основания, равна сумме внутренних углов, образующихся при пересечении параллельных прямых секущей, т.е. 180°.
Следовательно, сумма двугранных углов, прилежащих к ребрам обоих оснований, равна n•180°
Для примера рассмотрим четырехугольную призму АВСDD1А1В1С1
Сумма двугранных углов КМН+ТНМ = 180°,
а сумма всех двугранных углов 4-угольной призмы равна 180•4=720°
В правильном многоугольнике все стороны и углы равны.
Внутренний угол правильного n-угольника вычисляется по формуле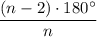
ΔABC = ΔBCD по двум сторонам и углу между ними (AB=BC=CD, ∠ABC=∠BCD), поэтому AC=BD, как соответственные стороны (AC напротив ∠ABC; BD напротив ∠BCD и эти углы равны).
ΔABD = ΔDCA по трём сторонам (AB=DC, AC=DB и AD - общая), поэтому ∠BAD=∠CDA, как соответственные углы (∠BAD напротив BD; ∠CDA напротив AC и эти стороны равны).
Сумма углов в выпуклом четырёхугольнике равна 360°.
В четырёхугольнике ABCD:
∠ABC+∠BCD+∠CDB+∠DAB = 360°
2·(∠BCD+∠CDA) = 360°
∠CDA = 360°:2-∠BCD = 180°-144° = 36°
ответ: 36°.