Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.
⇒ ЕК || ОМ || АС
2. Рассмотрим АВС.
АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)
⇒ ЕК - средняя линия (по определению)
Средняя линия равна половине основания.
⇒
3. Рассмотрим ΔАЕК.
АО = ОК; ОН || ЕК.
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.
Объяснение:
Дано: ΔАВС;
АК и СЕ - медианы;
СМ = МЕ; АО = ОК;
АС = а
Найти: ОМ.
1. СМ = МЕ; АО = ОК
Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.⇒ ЕК || ОМ || АС
2. Рассмотрим АВС.
АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)
⇒ ЕК - средняя линия (по определению)
Средняя линия равна половине основания.⇒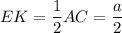
3. Рассмотрим ΔАЕК.
АО = ОК; ОН || ЕК.
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.⇒ ОН - средняя линия ΔАЕК.
4. Рассмотрим ΔЕКС.
СМ = МЕ; МР || ЕК;
⇒МР - средняя линия ΔЕКС.
5. Рассмотрим ΔАЕС.
АН = НЕ (п.3); НМ || AC
⇒ НМ - средняя линия ΔАЕС.
6. Рассмотрим ΔАКС.
КР = РС (п.4); ОР || АС;
⇒ ОР - средняя линия ΔАКС.
7.
1)Рисуешь небольшой квадрат, и имянуешь каждый угол по порядку так, как написано в условии.
получается:
а)От G до FE(не включительно) будет всего лишь :
GH=17см, т.к. просят отрезок именно FЕ, если бы просили ЕF, то было бы GH, HE =17+17=34см.
б)Центр квадрата намного легче посчитать, в отличие от круга.
Центр квадрата будет равен половине его любой стороны (все стороны равны), значит.
О=17:2=8,5см.
Если О действительно центр, то самое короткое расстояние от О до любой стороны будет его перпендикуляром, и в нашем случае будет равно 8,5 см.
ответ:а) 34см,б)8,5см.
Объяснение: