Стороны параллелограмма равны 5 см и 20 см, а высота, проведённая к большей стороне, равна 4,4 см. Вычисли высоту, проведённую к меньшей стороне.
Скольки равна высота, проведённая к меньшей стороне?
Зависит ли величина площади фигуры от того, по какой формуле площади она вычисляется?
Т.к. пирамида правильная, значит в основании лежит равносторонний треугольник АВС, в котором высота является и медианой и биссектрисой. Точкой Р обозначим точку, в которую опущена высота ВР этого треугольника. Высота делит АВС на два равных прямоугольных треугольника АВР и ВРС.
Пусть АВ=х - сторона основания пирамиды, тогда РС=х/2.
Тогда по теореме Пифагора х^2=(x/2)^2+3^2
или x^2=1/4*x^2+9. Отсюда находим х=корень из 12.
Тогда площадь равностороннего треугольника Sabc=1/2*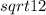 *
*![sqrt{12}[/tex*sin60=3[tex]sqrt{3}](/tpl/images/0167/6314/05f01.png)
Периметр треугольника Р=3*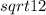
Тогда площадь полной поверхности пирамиды есть S=1/2PL+Sabc, где L - апофема
S=1/2*3*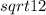 *4+3*
*4+3*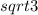 =15
=15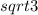
Для того что бы решить данную задачу нужно посмотреть на какую дугу опираются данные углы и вспомнить что вписанный угол равен половине центрального угла, а центральный угол равен величине дуги.
1) Угол ABC опирается на дугу AC, которая не включает в себя точки D и B. Величина данного угла равна 100 градусам.
2) Угол ACD опирается на дугу AD, которая не включает в себя точки C и B. Величина данного угла равна 80 градусам.
3) Угол DAC опирается на дугу DC, которая не включает в себя точку А. Величина данного угла равна ? градусам.
т.к полный круг равен 360 градусов то дуга DC равна 180, а значит угол DAC равен 90.