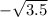Расстояние от точки А до точки, лежащей на кривой, должно быть наименьшим. Если в качестве точки на кривой взять точку с координатами (х;-√(-х+3)), то найдя это расстояние по формуле
√(х-х₀)²+(у-у₀)², проанализируем подкоренное выражение, и найдем координату у.
У нас А(х₀;у₀);В(х;у), значит, АВ=√((х-(-1))²+((-√(-х+3))-0)²)=
√(х²+2х+1+3-х)=√(х²+х+4) расстояние будет наименьшим, когда подкоренное выражение наименьшее. Но под корнем - квадратный трехчлен, у которого старший коэффициент равен 1, т.е. график - парабола, ветви которой направлены вверх, значит, наименьшее значение эта функция достигает в своей вершине, т.е. х=-b/2a=-1/2.
тогда у=-√((1/2)+3) =-√3.5
ответ ордината точки, ближайшей к точке А(-1;0), есть у=-√3.5
Так как необходимо найти ближайшую точку В к точке А, то расстояние АВ должно быть наименьшим.
Найдем, при каком значении х функция принимает наименьшее значение. Так как функция корня принимает наименьшее значение при наименьшем аргументе, то это произойдет, когда аргумент примет наименьшее значение. Значит, нужно найти, при каком значении х функция принимает наименьшее значение. Выделим полный квадрат:
Так как квадрат любой величины не принимает отрицательных значений, то наименьшее значение достигается при , то есть при - графически соответствует вершине параболы.
При функция принимает наименьшее значение, а значит и функция принимает наименьшее значение. Так как последняя функция соответствует расстоянию АВ, то именно в этом случае расстояние АВ будет наименьшим.
Расстояние от точки А до точки, лежащей на кривой, должно быть наименьшим. Если в качестве точки на кривой взять точку с координатами (х;-√(-х+3)), то найдя это расстояние по формуле
√(х-х₀)²+(у-у₀)², проанализируем подкоренное выражение, и найдем координату у.
У нас А(х₀;у₀);В(х;у), значит, АВ=√((х-(-1))²+((-√(-х+3))-0)²)=
√(х²+2х+1+3-х)=√(х²+х+4) расстояние будет наименьшим, когда подкоренное выражение наименьшее. Но под корнем - квадратный трехчлен, у которого старший коэффициент равен 1, т.е. график - парабола, ветви которой направлены вверх, значит, наименьшее значение эта функция достигает в своей вершине, т.е. х=-b/2a=-1/2.
тогда у=-√((1/2)+3) =-√3.5
ответ ордината точки, ближайшей к точке А(-1;0), есть у=-√3.5
Выберем на кривой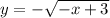 некоторую точку
некоторую точку 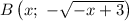 .
.
Найдем расстояние АВ:
Так как необходимо найти ближайшую точку В к точке А, то расстояние АВ должно быть наименьшим.
Найдем, при каком значении х функция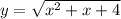 принимает наименьшее значение. Так как функция корня принимает наименьшее значение при наименьшем аргументе, то это произойдет, когда аргумент
принимает наименьшее значение. Так как функция корня принимает наименьшее значение при наименьшем аргументе, то это произойдет, когда аргумент 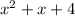 примет наименьшее значение. Значит, нужно найти, при каком значении х функция
примет наименьшее значение. Значит, нужно найти, при каком значении х функция 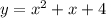 принимает наименьшее значение. Выделим полный квадрат:
принимает наименьшее значение. Выделим полный квадрат:
Так как квадрат любой величины не принимает отрицательных значений, то наименьшее значение достигается при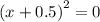 , то есть при
, то есть при  - графически соответствует вершине параболы.
- графически соответствует вершине параболы.
При функция
функция 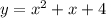 принимает наименьшее значение, а значит и функция
принимает наименьшее значение, а значит и функция 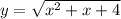 принимает наименьшее значение. Так как последняя функция соответствует расстоянию АВ, то именно в этом случае расстояние АВ будет наименьшим.
принимает наименьшее значение. Так как последняя функция соответствует расстоянию АВ, то именно в этом случае расстояние АВ будет наименьшим.
Найдем ординату точки В:
ответ: