Параллель түзулердің қиюшымен жасайтын екі ішкі айқыш
бұрыштардың қосындысы 150-қа тең. осы бұрыштарды
табыңдар.
​

1. Пусть х - угол при основании, тогда х+96 - угол при вершине, лежащей против основания. Углы при основании равнобедренного треугольника равны. Сумма углов треугольника равна 180°.

х + х + х+96 = 180

3х = 180 - 96

3х = 84

х = 28

ответ: 28°

2. Пусть k - коэффициент пропорциональности, тогда:

6k + 2k + 7k = 180

15k = 180

k = 12

∠А = 6k = 6 * 12 = 72°

∠В = 2k = 2 * 12 = 24°

∠М = 7k = 7 * 12 = 84°

3. Треугольник DEF - равнобедренный (так как FE=DE), ∠DEF - это угол, лежащий против основания, тогда:

∠EDF = (180 - ∠DEF)/2 = (180 - 27)/2 = 76,5°

В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.

S(осн.)=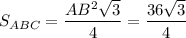 =9√3 см².

Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.

=√3 см

В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.

=√147 см

Боковые грани правильной пирамиды это равные треугольники.

S(бок.)=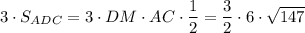 =9√147 см²

S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²

ответ: 9√3 + 9√147 см².