Даны вершины А(3; -1), B(2; 2), C(4; 1).
Вектор АВ: (-1; 3), вектор АС: (1; 2).
Уравнение прямой АВ: (х - 3)/(-1) = (у + 1)/3,
Общее уравнение АВ: 3х + у - 8 = 0.
Уравнение прямой АС: (х - 3)/(1) = (у + 1)2,
Общее уравнение АС: 2х - у - 7 = 0.
Точки на биссектрисе угла А равно удалены от сторон АВ и АС.
Используем формулу расстояния точки от прямой и приравняем расстояние до АВ и АС.
d=|Ax0+By0+C|/√(A²+B²).
Пусть точка на биссектрисе имеет координаты (х; у).
Находим значения √(A²+B²) для прямых АВ и АС.
Для АВ: √(3²+ 1²) = √10, для АС: √(2²+ (-1)²) = √5.
Получаем:
Раскроем модули. Для внутреннего угла А подходит уравнение с минусом:
Домножим числитель и знаменатель правой дроби на корень из 2 и приравняем числители.
Отсюда получаем ответ.
Уравнение биссектрисы угла А имеет вид:
х(3 + 2√2) + у(1 - √2) - (8 + 7√2) = 0.
Можно дать в цифровом виде: общее уравнение
Х - 0,071067812 У - 3,071067812 = 0 или с угловым коэффициентом: у = 14,07106781 х - 43,21320344 .
Даны вершины А(3; -1), B(2; 2), C(4; 1).
Вектор АВ: (-1; 3), вектор АС: (1; 2).
Уравнение прямой АВ: (х - 3)/(-1) = (у + 1)/3,
Общее уравнение АВ: 3х + у - 8 = 0.
Уравнение прямой АС: (х - 3)/(1) = (у + 1)2,
Общее уравнение АС: 2х - у - 7 = 0.
Точки на биссектрисе угла А равно удалены от сторон АВ и АС.
Используем формулу расстояния точки от прямой и приравняем расстояние до АВ и АС.
d=|Ax0+By0+C|/√(A²+B²).
Пусть точка на биссектрисе имеет координаты (х; у).
Находим значения √(A²+B²) для прямых АВ и АС.
Для АВ: √(3²+ 1²) = √10, для АС: √(2²+ (-1)²) = √5.
Получаем: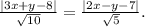
Раскроем модули. Для внутреннего угла А подходит уравнение с минусом: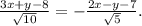
Домножим числитель и знаменатель правой дроби на корень из 2 и приравняем числители.
Отсюда получаем ответ.
Уравнение биссектрисы угла А имеет вид:
х(3 + 2√2) + у(1 - √2) - (8 + 7√2) = 0.
Можно дать в цифровом виде: общее уравнение
Х - 0,071067812 У - 3,071067812 = 0 или с угловым коэффициентом: у = 14,07106781 х - 43,21320344 .