8+2√10.
Объяснение:
По т.Пифагора (для ΔАDC):
АС²=AD²+DC²
AC²=((3√10)/5)²+(√10/5)²
AC²=(9*10/25)+(10/25)
AC²=90/25+(10/25)
AC²=100/25
AC²=4
AC=√4=2.
По теореме о высоте проведённой из прямого угла в прямоугольном треугольнике:
AD=
(AD)²=()²
AD²=BD*DC
BD=AD²/DC
BD=((3√10)/5)²/(√10/5)
BD=(9*10/25)/(√10/5)
BD=(90/25)/(√10/5)
BD=(90*5)/(25*√10)
BD=(90)/(5*√10)
BD=(9√10)/5
BC=BD+DC
BC=(9√10)/5+(√10/5)=2√10
По т.Пифагора (для ΔАВС):
ВС²=АС²+АВ²
(2√10)²=2²+АВ²
4*10=4+АВ²
АВ²=40-4
АВ²=36
АВ=√36=6.
РΔАВС=АВ+ВС+АС=6+2√10+2=8+2√10
8+2√10.
Объяснение:
По т.Пифагора (для ΔАDC):
АС²=AD²+DC²
AC²=((3√10)/5)²+(√10/5)²
AC²=(9*10/25)+(10/25)
AC²=90/25+(10/25)
AC²=100/25
AC²=4
AC=√4=2.
По теореме о высоте проведённой из прямого угла в прямоугольном треугольнике:
AD=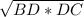
(AD)²=(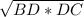 )²
)²
AD²=BD*DC
BD=AD²/DC
BD=((3√10)/5)²/(√10/5)
BD=(9*10/25)/(√10/5)
BD=(90/25)/(√10/5)
BD=(90*5)/(25*√10)
BD=(90)/(5*√10)
BD=(9√10)/5
BC=BD+DC
BC=(9√10)/5+(√10/5)=2√10
По т.Пифагора (для ΔАВС):
ВС²=АС²+АВ²
(2√10)²=2²+АВ²
4*10=4+АВ²
АВ²=40-4
АВ²=36
АВ=√36=6.
РΔАВС=АВ+ВС+АС=6+2√10+2=8+2√10