В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
1) Для нахождения координат требуется решить систему данных уравнений. Из второго уравнения находим x=3y-4, Подставляя это выражение для x в первое уравнение, получаем уравнение 4-3y+2y-4=-y=0, откуда y=0. Подставляя найденное значение y в любое из данных уравнений, находим x=-4. Таким образом, точка пересечения прямых имеет координаты (-4,0). 2) У любой точки первой четверти обе координаты положительны, у точек 2 четверти x<0, y>0, у точек 3 четверти x<0,y<0, у точек 4 четверти x>0,y<0. У точки С x>0, y<0. Поэтому точка С расположена в 4 координатной четверти.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=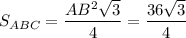
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=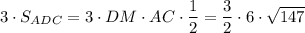
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
2) У любой точки первой четверти обе координаты положительны, у точек 2 четверти x<0, y>0, у точек 3 четверти x<0,y<0, у точек 4 четверти x>0,y<0. У точки С x>0, y<0. Поэтому точка С расположена в 4 координатной четверти.