Напишите теорему,обратную данной теореме и проверьте верно ли обратное утверждение. •Если две прямые пересекаются под прямым углом,то такие прямые называются перпендикулярными.

Расстояние от моста до пристани катер преодолел на 2 часа быстрее, чем расстояние от пристани до моста. Найдите собственную скорость катера, если скорость течения 2 км/ч, а расстояние между пристанью и мостом 48 км.

Объяснение:

Пусть собственная скорость катера х км/ч , х>0,

тогда скорость катера против течения (х-2) км/ч.  ,

а скорость по течению (х+2) км/ч .

Время катера против течения 48/(х-2) ч,

а время катера по течению 48/(х+2) км/ч.

Т.к время катера против течения на 2 часа больше , то составим уравнение : ,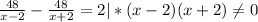

48(х+2)-48(х-2)=2(х-2)(х+2) ,

49х+96-48х+96=2х²-8,

2х²=192+8,

х²=100 ⇒ х=10.

ответ. Собственная скорость катера 10 км/ч.

1.

Найдем второй катет первого треугольника. Теорема Пифагора, квадрат гипотенузы равен сумме квадратов катетов

a²=5²-4²

a²=25-16

a²=9

a=√9

a=3

Второй катет 3

Сумма внутренних углов треугольника 180°.

У первого треугольника один угол 90°, второй 53°. Найдем меньший угол первого треугольника.

180°-90°-53°=37°.

Теперь найдем гипотенузу второго треугольника по теореме Пифагора.

c²=24²+18²

c²=576+324

c²=900

c=√900

c=30

Разделим все стороны второго на соответственные (больший делим на большую сторону, меньший на меньшую и т.д.) стороны первого.

Так как они все пропорциональны (признак подобия треугольников), эти два треугольника подобные, то есть углы одинаковые. Следовательно, меньший угол второго треугольника тоже 37°.

2.

Найдем катет первого треугольника по теореме Пифагора

a²=10²-8²

a²=100-64

a²=36

a=√36

a=6

Во втором треугольнике найдем гипотенузу по той же теореме.

c²=12²+16²

c²=144+256

c²=400

c=√400

c=20

Разделим соответственные стороны второго на первый:

Все стороны пропорциональны, значит они подобные. Меньший угол второго треугольника 36°.