между сторонами угла aob равного 134 градуса проведены лучи oc и om так, что угол aoc на 26 градусов меньше угла boc а om биссектриса угла boc. Найдите величину угла com. ответ дайте в градусах
Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
, 7х=14*4 , х=8. Поэтому МО₁ =14-8=6.
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная α, касается меньшего шара, а площадь сечения большего шара этой плоскостью равна 5.(бедные дети) Найдите площадь сечения большего шара плоскостью α.
Объяснение:
Рассмотрим сечение данной комбинации тел и плоскостей , проходящее через диаметры шаров и перпендикулярно секущим плоскостям α и β. Пусть радиусы большого шара R ,малого шара r.
Объяснение:
Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
ΔМО₁С₁ -прямоугольный, tg∠МС₁О₁ =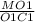
=
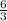⇒ tg∠МС₁О₁=2.
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная α, касается меньшего шара, а площадь сечения большего шара этой плоскостью равна 5.(бедные дети) Найдите площадь сечения большего шара плоскостью α.
Объяснение:
Рассмотрим сечение данной комбинации тел и плоскостей , проходящее через диаметры шаров и перпендикулярно секущим плоскостям α и β. Пусть радиусы большого шара R ,малого шара r.
S(кр)=πr² , S(крАС)=5 ⇒ АС=√5/π, S(крКВ)=7 ⇒ КВ=√7/π.
В сечении большего шара плоскостью α получаем круг с радиусом КМ , S(КМ)= π* КМ² .
ΔМКО-прямоугольный , R²= КМ²+КО² (1)
ΔВКО-прямоугольный , r²= КВ²+КО² (2). Вычтем из (1) уравнения (2).
R²-r²=КМ²-КВ² (3).
ΔАСО-прямоугольный , ОА²=СО²+АС² или R²=r²+АС² или
R²- r²= АС² подставим в (3).
АС²=КМ²-КВ² или КМ²=АС²+КВ²
КМ²=(√5/π)²+(√7/π)²=12/π
S(КМ)= π* КМ²=π*12/π=12 (ед²).