Формула вычисления длины окружности, зная радиус окружности:
Для начала определим вид треугольника.
Нам уже дано, что около трапеции однозначно описана окружность.
А окружность можно описать только около равнобедренной трапеции!.
Что и означает, что боковые стороны равны — 6; 6.
Другого выбора у нас нет, кроме как объявить, что одно из оснований ровно боковой стороне — 6, а второе основание равно: 12.
Формула вычисления радиусa описанной окружности около равнобёдренной трапеции — такова:
Тоесть, для вычисления этого радиуса — нам должны быть известны основания трапеции, боковая сторона, и! диагональ.
Обозначения сторон: боковые равные стороны равны: "c"; большее основание равно: "b"; меньшее основание равно: "b".
Формула вычисления диагонали равнобедренной трапеции такова:
А в этой формуле, переменные таковы: обе боковые стороны обозначаются как "a"; верхнее основание, которое равно боковой стороне — обозначается как "b"; основание с длиной в 12 см — обозначается как "c".
Теперь, зная все стороны трапеции, и диагональ — найдём радиус:
Если третья сторона будет=1 см, то не получится неравенство: 1см+1см= 2 см, тогда 3см>2 см, а должно быть<. Если третья сторона = 2 см, то неравенство опять не получится: 2+1=3, тогда 3=3, так тоже не может быть, т.к. одна из сторон треугольника должна быть меньше суммы двух других сторон. Если третья сторона =3 см, тогда 1+3=4, 3<4, неравенство выполняется, 3+3=6, 3<6- неравенство получается. Возьмем 4 см: 3+1=4, 4=4- не получается, значит и в последующих числах не получится. ответ: 3 см
Формула вычисления длины окружности, зная радиус окружности: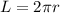
Для начала определим вид треугольника.
Нам уже дано, что около трапеции однозначно описана окружность.
А окружность можно описать только около равнобедренной трапеции!.
Что и означает, что боковые стороны равны — 6; 6.
Другого выбора у нас нет, кроме как объявить, что одно из оснований ровно боковой стороне — 6, а второе основание равно: 12.
Формула вычисления радиусa описанной окружности около равнобёдренной трапеции — такова:
Тоесть, для вычисления этого радиуса — нам должны быть известны основания трапеции, боковая сторона, и! диагональ.
Обозначения сторон: боковые равные стороны равны: "c"; большее основание равно: "b"; меньшее основание равно: "b".
Формула вычисления диагонали равнобедренной трапеции такова: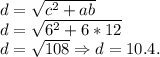
А в этой формуле, переменные таковы: обе боковые стороны обозначаются как "a"; верхнее основание, которое равно боковой стороне — обозначается как "b"; основание с длиной в 12 см — обозначается как "c".
Теперь, зная все стороны трапеции, и диагональ — найдём радиус: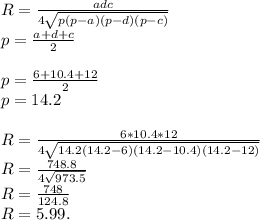
Теперь, зная радиус — найдём длину окружности:
Вывод: L = 37.63.