Словосочетание — это сочетание двух (или более) самостоятельных слов, связанных между собой подчинительной связью по смыслу и грамматически: читать книгу, теплый день.
Словосочетания называют предметы, действия, признаки и т. д. , но более точно, более конкретно, чем слова: читать — читать вслух, ручка — шариковая ручка, быстро — очень быстро.
Словосочетание состоит из главного и зависимого слова.
Слово, которое называет предмет, признак, действие и т. д. , называется главным. Слово, которое поясняет, распространяет главное, называется зависимым. От главного слова к зависимому можно задать вопрос.
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
Итак, Р(3,4,1) . Следовательно,
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
Словосочетания называют предметы, действия, признаки и т. д. , но более точно, более конкретно, чем слова: читать — читать вслух, ручка — шариковая ручка, быстро — очень быстро.
Словосочетание состоит из главного и зависимого слова.
Слово, которое называет предмет, признак, действие и т. д. , называется главным.
Слово, которое поясняет, распространяет главное, называется зависимым.
От главного слова к зависимому можно задать вопрос.
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
Итак, Р(3,4,1) . Следовательно,
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
ВЫЧИСЛИМ ПЕРИМЕТР ПИРАМИДЫ: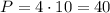 .
.
Вычислим площадь боковой поверхности пирамиды: