а) Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено условие: боковые ребра пирамиды равны.
Длины сторон
AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 6 0 0 36 6
BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²) = -3 5,19615 0 36 6
CD = √((xD-xC)²+(yD-yC)²+(zD-zC)²) = 0 -3,46410 2 16 4
AD = √((xD-xA)²+(yD-yA)²+(zD-zA)² = 3 1,73205 2 16 4
AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²) = 3 5,19615 0 36 6
BD = √((xD-xB)²+(yD-yB)²+(zD-zB)²) = -3 1,73205 2 16 4 .
Как видим, в основании правильный треугольник и все боковые рёбра равны. Значит, пирамида правильная.
б) Основание апофемы пирамиды,лежащей в грани DAC, это середина стороны основания АС - точка Е.
Даны точки A(-1;0;1), C(2;3√3;1)
Е = ((-1+2)/2); (0+3√3)/2); ((1+1)/2)) =((-1/2); (3√3/2); 1).
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD= =10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD= =135°
а) Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено условие: боковые ребра пирамиды равны.
Длины сторон
AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 6 0 0 36 6
BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²) = -3 5,19615 0 36 6
CD = √((xD-xC)²+(yD-yC)²+(zD-zC)²) = 0 -3,46410 2 16 4
AD = √((xD-xA)²+(yD-yA)²+(zD-zA)² = 3 1,73205 2 16 4
AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²) = 3 5,19615 0 36 6
BD = √((xD-xB)²+(yD-yB)²+(zD-zB)²) = -3 1,73205 2 16 4 .
Как видим, в основании правильный треугольник и все боковые рёбра равны. Значит, пирамида правильная.
б) Основание апофемы пирамиды,лежащей в грани DAC, это середина стороны основания АС - точка Е.
Даны точки A(-1;0;1), C(2;3√3;1)
Е = ((-1+2)/2); (0+3√3)/2); ((1+1)/2)) =((-1/2); (3√3/2); 1).
Трапеция ABCD с основанием AD вписана в окружность с центром О.Найдите углы трапеции,если ∠AOD=100°,∠BOC=80° и точка О лежит вне трапеции.
Объяснение:
Вписанная в окружность трапеция является равнобедренной.
Значит АВ=CD стягивают равные дуги → ∪AB=∪CD
∠BOC=80° -центральный → ∪ВС=80°
∠AOD=100°--центральный → ∪АВD=100° ⇒ ∪AB=∪CD=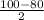 =10°.
=10°.
∠BAD вписанный и опирается на дугу ∪BCD=∪BC+∪CD=80°+10°=90°.
∠BAD=1/2*90°=45°. Значит ∠СDA=45° и ∠СВA=45° (углы при основании равны )
Сумма углов 4-х угольника 360°. Поэтому ∠АВС=∠ВСD=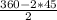 =135°
=135°