Дан прямоугольный треугольник Abc с катетами BC=a, Ac=b. D- точка пересечения биссектрисы угла B и серединного перпендикуляра к отрезку AC. Найдите площадь треугольника BCD​

Дана правильная шестиугольная пирамида.
Сторона а основания равна апофеме А.
Найти угол между боковой гранью и основанием.
Примем длину стороны и апофемы за 1.
Дано: Сторона основания а = 1 Апофема А = SM = 1

Проекция апофемы на основание - это радиус вписанной окружности r(o)впис = OM = a*cos 30° = 1*(√3/2) ≈ 0,866025.
Высота H пирамиды равна:
H = √(A² - r²) = √(1² - (√3/2)²) = 1/2.
Тангенс угла наклона двугранного угла между боковой гранью и основанием равен плоскому углу в плоскости, перпендикулярной линии пересечения плоскостей, то есть к ребру пирамиды.
tg a = H/r = 0,5/(√3/2) = 1/√3 ≈ 0,523599.
Этому тангенсу соответствует угол 30  градусов.

Вариант 1

№1.  Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.

Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора:  BC = = = =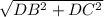

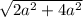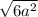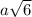
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.

DC = DB = a : sin45 =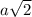

Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.

DB = DC = BC =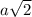

(Дальше долко)