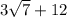Четырёх угольник авсд вписан в окружность радиуса 8. известно ав=вс=сд=12. доказать. что вс и ад параллельны. найти ад. указание. возможно понадобится найти синус 3х. его можно найти через сумму синусов х и 2х.
1) Т.к. углы CDB и CAB опираются на одну и ту же дугу, то они равны. Тогда треугольники DCB и ABC равны по стороне и 2-м углам(AC общая, а углы CDB=DBC=CAB=BAC т.к. треугольники DCB и ABC равнобедренные и углы CDB=CAB см. выше). Треугольники DCA и ABD равны по тому же принципу. В итоге треугольники CTB и DTA равнобедренные, а т.к. углы CTB и DTA вертикальные, то углы TDA и TBC равны, а это признак параллельности прямых, тогда CB || AD.
2) Пусть ACB=α. По формуле радиуса описанной окружности , тогда . Угол DCA=180-3α. По теореме синусов имеем . Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось
1) Т.к. углы CDB и CAB опираются на одну и ту же дугу, то они равны. Тогда треугольники DCB и ABC равны по стороне и 2-м углам(AC общая, а углы CDB=DBC=CAB=BAC т.к. треугольники DCB и ABC равнобедренные и углы CDB=CAB см. выше). Треугольники DCA и ABD равны по тому же принципу. В итоге треугольники CTB и DTA равнобедренные, а т.к. углы CTB и DTA вертикальные, то углы TDA и TBC равны, а это признак параллельности прямых, тогда CB || AD.
2) Пусть ACB=α. По формуле радиуса описанной окружности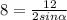 , тогда
, тогда  . Угол DCA=180-3α. По теореме синусов имеем
. Угол DCA=180-3α. По теореме синусов имеем 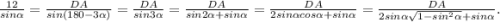 . Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось
. Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось