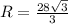Abcd-прямоугольная трапеция, ck параллельно ab, kd=9см, ab относится к cd как 4: 5. найдите площадь abcd.

Показать ответ

Ответ:

ancelina1234

13.05.2020 17:03

Равносторонних трапеций не бывает, скорее всего имеется в виду равнобокая трапеция (с равными боковыми сторонами).

Если одну из диагоналей перенести в общую вершину со второй диагональю, то получим равнобедренный прямоугольный треугольник с прямым углом вверху и углами по 45 градусов у нижнего основания.

Тогда легко находится высота треугольника - она и высота трапеции.

Высота равна половине гипотенузы нового треугольника, которая равна 16 + 20 = 36 см.

ответ: длина высоты трапеции равна 36/2 = 18 см.

0,0(0 оценок)

Ответ:

milanareemets

09.07.2021 12:00

Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.

Для треугольника ABD воспользуемся теоремой синусов и получим

$\frac{BD}{sinA} =2R$

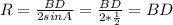
То есть $R = \frac{BD}{2sinA} =\frac{BD}{2*\frac{1}{2} }=BD$

Даже вот так. Радиус этой окружности равен длине стороны BD.

Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD

Тогда AD = AH + HK + KD = 2*AH + HK

BCKH - прямоугольник, BC = HK = 12

AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4

HD = HK + KD = 12 + 4 = 16

Не хватает стороны BH. Её можно найти из треугольника ABH

$ctgA = \frac{AH}{BH}; \sqrt{3} = \frac{4}{BH}; BH = \frac{4}{\sqrt{3} } =\frac{4\sqrt{3} }{3}$

Теперь по теореме Пифагора ищем BD

BD^2 = BH^2 + HD^2

$BD^2 = \frac{16}{3}+16^2 = \frac{16+3*16^2}{3}=\frac{16}{3}(1+3*16)=\frac{16}{3}*49\\ BD = \sqrt{\frac{4^2*7^2}{3} }=\frac{4*7}{\sqrt{3}} = \frac{28}{\sqrt{3} } =\frac{28\sqrt{3} }{3}$