∠ACD =∪AC/2 =∠ABC (угол между касательной и хордой)
△ACD~△CBD (по двум углам, ∠D - общий)
AC/CB =CD/BD =AD/CD
AC/CB =AM/MB =9/12 =3/4 (по теореме о биссектрисе)
BD=4/3 CD, AD=3/4 CD
BD-AD=AB => 4/3 CD -3/4 CD =21 <=> CD=21*12/7 =36
Или
∠ACD =∪AC/2 =∠B =>
∠DCM =∠ACD+∠C/2 =∠B+∠C/2 =∠DMC
△CDM - равнобедренный, DC=DM
Квадрат касательной равен произведению секущей на ее внешнюю часть.
DC^2 =DB*DA
DA=DM-AM, DB=DM+MB
DC^2 =(DC+MB)(DC-AM) <=>
DC^2 =DC^2 +MB*DC -AM*DC -AM*MB <=>
DC=AM*MB/(MB-AM) =9*12/(12-9) =36
Для начала необходимо привести уравнение окружности к стандартному виду: (x-a)²+(y-b)²=r² , где (a;b) - центр , r - радиус.
Для этого свернём выражение как 2 квадрата разности
Думаю, это нужно сделать детально.
x²-10x=(x-5)²-25
y²-2y=(y-1)²-1
20=20
Если сложить все 3 уравнения, то получится:
x²+y²-10x-2y+20=(x-5)²-25+(y-1)²-1+20. Так как начальное выражение(слева) было равно 0, то и правая часть тоже. Имеем:
(x-5)²-25+(y-1)²-1+20=0
(x-5)²+(y-1)²=6 Отсюда видим, что центр окружности (5;1) , а радиус √6
Значит нам нужна прямая, параллельная y=7x-2.
Прямые параллельны, если у них одинаковый угловой коэффициент(цифра перед х)
Запишем уравнение прямой в общем виде
y=kx+m. Мы знаем угловой коэффициент и точку, принадлежащую прямой(центр окружности). Подставим всё
1=7*5+m ⇔ m= -34
Итого имеем - уравнение нашей прямой
∠ACD =∪AC/2 =∠ABC (угол между касательной и хордой)
△ACD~△CBD (по двум углам, ∠D - общий)
AC/CB =CD/BD =AD/CD
AC/CB =AM/MB =9/12 =3/4 (по теореме о биссектрисе)
BD=4/3 CD, AD=3/4 CD
BD-AD=AB => 4/3 CD -3/4 CD =21 <=> CD=21*12/7 =36
Или
∠ACD =∪AC/2 =∠B =>
∠DCM =∠ACD+∠C/2 =∠B+∠C/2 =∠DMC
△CDM - равнобедренный, DC=DM
Квадрат касательной равен произведению секущей на ее внешнюю часть.
DC^2 =DB*DA
DA=DM-AM, DB=DM+MB
DC^2 =(DC+MB)(DC-AM) <=>
DC^2 =DC^2 +MB*DC -AM*DC -AM*MB <=>
DC=AM*MB/(MB-AM) =9*12/(12-9) =36
Для начала необходимо привести уравнение окружности к стандартному виду: (x-a)²+(y-b)²=r² , где (a;b) - центр , r - радиус.
Для этого свернём выражение как 2 квадрата разности
Думаю, это нужно сделать детально.
x²-10x=(x-5)²-25
y²-2y=(y-1)²-1
20=20
Если сложить все 3 уравнения, то получится:
x²+y²-10x-2y+20=(x-5)²-25+(y-1)²-1+20. Так как начальное выражение(слева) было равно 0, то и правая часть тоже. Имеем:
(x-5)²-25+(y-1)²-1+20=0
(x-5)²+(y-1)²=6 Отсюда видим, что центр окружности (5;1) , а радиус √6
2)Значит нам нужна прямая, параллельная y=7x-2.
Прямые параллельны, если у них одинаковый угловой коэффициент(цифра перед х)
Запишем уравнение прямой в общем виде
y=kx+m. Мы знаем угловой коэффициент и точку, принадлежащую прямой(центр окружности). Подставим всё
1=7*5+m ⇔ m= -34
Итого имеем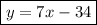 - уравнение нашей прямой
- уравнение нашей прямой