Знайдіть два послідоних натуральних числа, добуток яких на 36 більший за менше з них

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .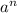

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .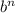

Рассмотрим многочлен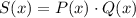 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :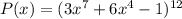

- степень определяется выражением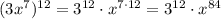 , то есть степень равна 84

- свободный член равен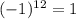

Для многочлена :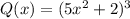

- степень определяется выражением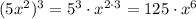 , то есть степень равна 6

- свободный член равен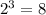

Наконец, для многочлена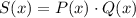 получим:

- степень определяется выражением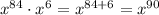 , то есть степень равна 90

- свободный член равен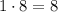

Сумма степени и свободного члена многочлена :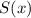

ответ: 98

ответ: 50 м и 60 м

Объяснение: Пусть длина участка x м, а ширина - y м, тогда площадь участка равна xy, а периметр равен 2·(x + y).

Составим систему уравнений:

xy = 3000

2x + 2y = 220

Второе уравнение разделим на 2:

xy = 3000

x + y = 110

Решим систему подстановки:

xy = 3000

x = 110 - y

(110 - y)·y = 3000

110y - y² = 3000

-y² + 110y - 3000 = 0

y² - 110y + 3000 =0

D = b² - 4ac = (-110)² - 4·3000 = 12100 - 12000 = 100

x₁ = 110 + √100  /  2  =  110 +10  /  2  =  60

x₂ = 110 - 10 /  2  = 50

y₁ = 110 - 60  = 50

y₂ = 110 - 50 = 60

Решением системы являются две пары чисел (60; 50) и (50; 60). Следовательно, стороны прямоугольника равны 50м и 60м.