Объяснение:
(x-1)(2x-2)<(2x-1)(x+2)
2x^2-2x-2x+2<2х^2+2х-х-2
2x^2-2x-2x-2х^2-2х+х<-2-2
-5х<-4
-х<-0,8
х>0,8
ответ:(0,8;+бесконечность)
x-1)(2x-2)<(2x-1)(x+2)
Объяснение:
(x-1)(2x-2)<(2x-1)(x+2)
2x^2-2x-2x+2<2х^2+2х-х-2
2x^2-2x-2x-2х^2-2х+х<-2-2
-5х<-4
-х<-0,8
х>0,8
ответ:(0,8;+бесконечность)
x-1)(2x-2)<(2x-1)(x+2)
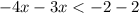
Х> 4/7